skip to content

Leverage Lending Algorithm of Euler

By 0xstan & 0xmc

欧拉协议杠杆借贷的算法

Liquidity

借贷协议中的 Liquidity 概念首先由 Compound 提出 Account Liquidity，即用户每一种进入 Markets 的资产都需要乘以相应的 Collateral Factor 累加起来，然后扣除用户每一种借贷资产的价值总和。

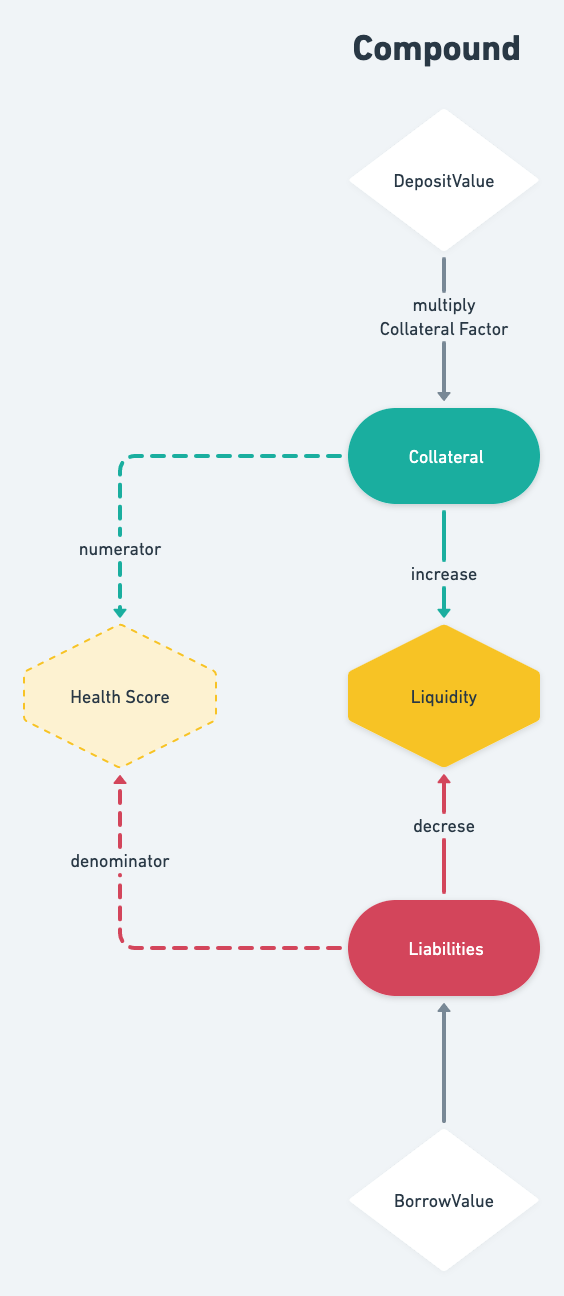
Euler-ComputeLiquidity.png

而 Euler 中的 Liquidity 在 Compound 基础上做改进，不仅抵押资产计算价值时需要乘以 CF (Collateral Factor)，债务资产也需要除以 BF (Borrow Factor) 做风险价值调整；另外由于其特有的 mint 机制，在计算时还需要考虑 Self_Collateral 和 Self_Liability。

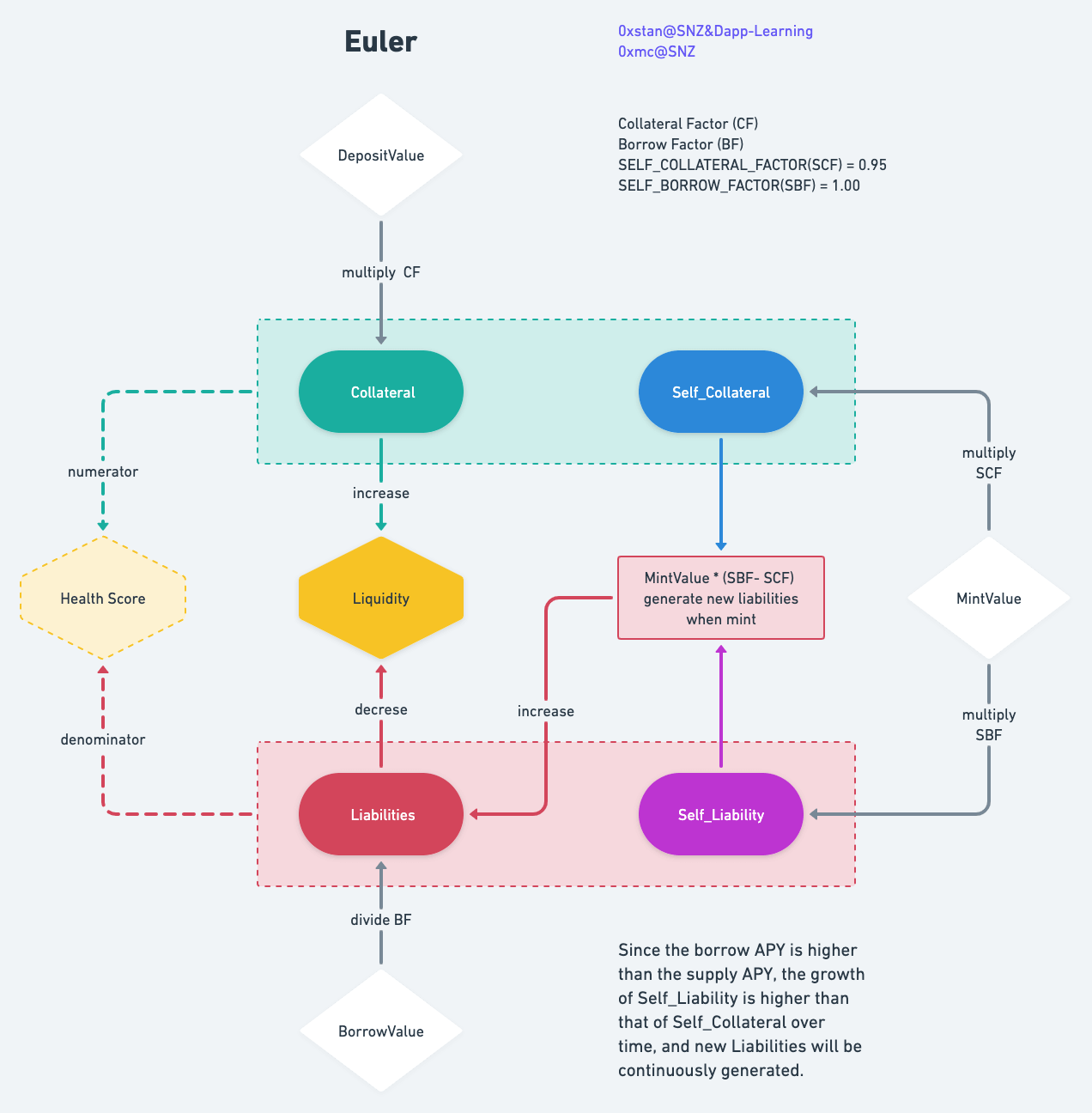
Euler-ComputeLiquidity.png

可以点击这里查看大图 Euler-Liquidity

注意资产价值都需要乘以一个风险价值调整因子，上述四个部分的调整系数都不同，下文中将详细介绍，为了方便起见我们将之后本文出现的所有经过风险系数调整后的资产价值后缀标记为_RiskAdjusted，简写为 _RA。

Liquidity=CollateralRA−LiabilitiesRA+(SelfCollateralRA−SelfLiabilityRA)Liquidity = Collateral_{RA} - Liabilities_{RA} + (Self_{Collateral_{RA}} - Self_{Liability_{RA}})

Self_Collateral 和 Self_Liability，这两者的调整价值 RiskAdjusted 在 Euler 的算法机制下总是会保持一致，即 self 部分的抵押和负债两者的风险调整价值会相互抵消 (两者流动性相减为 0)，所以实际上 Liquidity 的表达最终如下：

Liquidity=CollateralRA−LiabilitiesRALiquidity = Collateral_{RA} - Liabilities_{RA}

HealthScore

健康系数，与 Compound 类似，是总抵押价值和负债价值的价值，两者都经过风险价值调整因子 factor 调整，不同资产的抵押和借贷的 factor 不同（CF, BF）。当抵押与借贷相等，HealthScore 为 1，处于临界点，一旦小于 1 则可以被清算。

Self_Collateralization

区别于其他的借贷协议，Euler 独有的 Self_Collateralization 概念，允许用户使用杠杆做空或者挖矿。

抵押资产分为 Collateral (前端页面中命名为 Supply) 和 Self_Collateral, 负债资产分为 Liabilities 和 Self_Liability，四种资产均有不同的价值风险价值调整因子 factor， 经过调整之后的资产价值为 RiskAdjusted。

CollateralfactorRiskAdjustedinfo
Collateral(DepositValue)CFvalue * CFdecided by governance
Self_CollateralSCFvalue * SCFconstant value 0.95
Liabilities(BorrowValue)BFvalue / BFdecided by governance
Self_LiablitySBFvalue / SBFconstant value 1
  • 常规抵押和负债 (Collateral, Liabilities)，CF, BF 都是小于 1 的数，前者比后者小
    • Euler 在 Compound 的 CF 基础上增加了 BF，使得不同资产之间的风险调整更加灵活
    • Euler risk-factors-list
  • mint 操作会产生等价值的的抵押和债务，即价值都为 MintValue 的 Self_Collateral 和 Self_Liability
  • self 部分的资产价值调整系数都是固定值，Self_Collateral 的风险价值调整因子 SCF 固定为 0.95， Self_Liabilities 的风险价值调整因子 SBF 固定为 1，那么经过风险价值因子调整后的负债与抵押的资产价值关系是：
    • Self_Collateral * SCF = Self_Liability / SBF
    • Self_Collateral 是和 MintValue 等值的抵押，但因为需要乘以 0.95 的风险价值调整因子，固只能抵消 0.95 倍的债务
    • 而还有 0.05 倍的 MintValue 债务被直接计入了 Liablities

Compute Liquidity

Euler 的所有资产都是以 WETH 计价，并从相应资产与 WETH 组成的交易对的 UniswapV3Pool 中获取 TWAP 价格，WETH 的价格恒等于 1。

假设当下 USDC 的价格是 1/3000 WETH，我们将设想几种不同的场景，从易到难梳理计算流动性的逻辑：

symbolCFBF
USDC0.90.94
WETH0.880.91

case 1

用户 deposit 了 3000 USDC，那么 DepositValue 为 3000*(1/3000) = 1 WETH，并未产生债务

  • Liquidity 非常好计算，只需考虑 Collateral_RA，即为抵押的 USDC 经过风险价值调整后的价值
  • Liquidity = Collateral_RA = DepositValue * CF = 1 * 0.9 = 0.9

case 2

用户 deposit 了 3000 USDC，DepositValue 为 1 WETH，并 borrow 0.5 WETH， BorrowValue 是 0.5 WETH

  • Liquidity 将是 Collateral_RA - Liabilities_RA
  • Liquidity = DepositValue * CF - BorrowValue / BF = 1 * 0.9 - 0.5 / 0.91 = 0.3505
  • 上述情况 Liquidity 还有盈余
  • 显然，当用户的 Liquidity 为 0 时，用户的健康系数达到被清算临界点 1，而用户此时 BorrowValue 达到最大值 DepositValue * CF * BF = 1 * 0.9 * 0.91 = 0.819

case 3

用户 deposit 了 3000 USDC，DepositValue 为 1 WETH，然后 mint 出 2 WETH，MintValue 为 2 WETH

  • 由于 mint 操作会产生等量的债务和抵押，得到价值都为 2 WETH 的抵押和负债，所以用户的债务和抵押的底层资产价值 （UnderlyingValue） 将各增加 MintValue(2 WETH)
  • Self_Collateral = MintValue = 2 WETH
  • 而调整后价值为 Self_Collateral_RA = MintValue * SCF = 2 * 0.95 = 1.9 WETH，SCF 是常量系数 0.95
  • Self_Liability_RA = Self_Collateral * SCF / SBF = 2 * 0.95 / 1 = 1.9 WTH , SBF 是常量系数 1
  • Liquidity 将是 Collateral_RA - Liabilities_RA + (Self_Collateral_RA - Self_Liability_RA)
  • (Self_Collateral_RA - Self_Liability_RA) 由于 self 部分债务和抵押的调整价值总是相互抵消的，所以这部分的 Liquidity 总是为 0
  • 需要注意的是，mint 出的债务只有 0.95 倍的债务被 Self_Collateral_RA 所抵消，仍有 MintValue * (1 - SCF) 价值的债务价值需要计入 Liabilities_RA
  • Collateral_RA = DepositValue * CF = 1 * 0.9
  • Liabilities_RA = MintValue * (1 - SCF) / BF = 2 * (1 - SCF) / BF
  • Liquidity = Collateral_RA - Liabilities_RA = 1 * 0.9 - 2 * (1 - 0.95) / 0.91 = 0.7901

case 4

用户 deposit 3000 USDC，DeositValue 是 1 WETH，然后调用 mint 操作， MintValue 为 2 WETH，接着 borrow 0.5 WETH

  • 本次在 case 3 的情况下再 borrow 0.5 WETH，只需要按照常规债务计算这部分新增的债务即可
  • Liquidity = 0.7901 - 0.5 / BF = 0.2406

case 5

用户 deposit 1500 USDC + 0.5 WETH， DepositValue 总计 1 WETH， mint 12 WETH， 分别生成了价值都是 12 WETH 的 Self_Collateral 和 Self_Liability

  • 我们在 case 3 中描述过两个 self 的抵押和债务相互抵消的过程，此处同理，self 部分相互抵消， Liabilities_RA 将增加 MintValue * (1 - SCF) = 12 * (1 - 0.95) = 0.6 WETH
  • 由于 deposit 只存入了 0.5 WETH， 那么 WETH 的 Collateral_RA = 0.5 * 0.88 = 0.44 WETH, 而 Liabilities_RA = 0.6 / 0.91 = 0.6593
  • WETH 部分的 Collateral 最终只能承担 0.44 WETH 的债务，剩下的 0.6593 - 0.44 = 0.2193 WETH 债务则需要由 USDC 的 Collateral_RA 承担，用户在 WETH 资产上的 Liquidity 已经清零
  • 而 USDC 的流动性则为 Liquidity_USDC = 0.5 * 0.9 - 0.2193 = 0.2307
  • 由于 WETH 流动性已经为 0，那么总的流动性即为 USDC 的流动性 Liquidity = 0.2307 WETH

case 6

我们在 case 3 的基础上考虑累计利息的因素，用户在 A 时刻 deposit 3000 USDC， DepositValue 1 WETH，然后 mint 2 WETH， MintValue 2 WETH，之后经过一年来到 B 时刻，抵押和债务各有不同利息累计

  • 假设两种资产的抵押和借贷的 APY 如下：

    symbolDeposit APYBorrow APY
    USDC2%6%
    WETH6%9%

  • DepositValue_B = DepositValue_A * (1 + 2%) = 1 * 1.02 = 1.02

  • LiabilitiesValue_B = Liabilities_A * (1 + 6%) = 0.1 * 1.06 = 0.106

  • Self_Collateral_B = Self_Collateral_A * (1 + 6%) = MintValue * 1.06

  • Self_Liability_B = Self_Liability_A * (1 + 9%) = MintValue * 1.09

  • 当时刻 A 用户 mint 之后， self 部分的抵押和债务价值相等 （相互抵消）即 Self_Collateral_A = Self_Liability_A ，当来到时刻 B 两者由于 APY 不同，价值将不再相等，通常债务的利息增长会更多，超出的债务部分则计入 Liabilities_RA

  • delta_Liabilities_RA = Self_Liability_B - Self_Collateral_B = MintValue * (1.09 - 1.06) / BF = 2 * 0.03 / 0.91 = 0.0659

  • Liabilities_RA_B = Liabilities_RA_A * (1 + 6%) + delta_Liabilities_RA = 0.106 + 0.0659 = 0.1719

  • Liquidity_B = Collateral_RA_A - Liabilities_RA_B = 1.02 * 0.9 - 0.1719 = 0.7461

Max Mint Leverage

假设用户在 deposit 操作之后，只进行 mint 操作，用户没有单独进行 borrow 操作，债务可以表示为：

LiabilitiesRA=MintValue∗(1−SCF)Liabilities_{RA} = MintValue * (1 - SCF)

将上述等式转换为 MintValue 的表达式：

MintValue=LiabilitiesRA/(1−SCF)MintValue = Liabilities_{RA} / (1 - SCF)

MintValue 的最大值由 Liabilities_RA 决定，即当 Liabilities_RA 最大时 Liquidity 为 0，HealthScore 已经变成 1，处于将要被清算的临界点，Liabilities_MAX_RA = Collateral_RA，那么此时 MintValue 即为最大值 MintValueMax。

MintValueMax=LiabilitiesMaxRA/(1−SCF)=CollateralRA/(1−SCF)MintValueMax = LiabilitiesMax_{RA} / (1 - SCF) = Collateral_{RA} / (1 - SCF)

此时用户拥有最多数量的 Self_Collateral 和 Self_Liability （mint 数量如果再增加，合约则会报错不能执行）。

SelfCollateral=MintValueMax=CollateralRA/(1−SCF){SelfCollateral} = MintValueMax = Collateral_{RA} / (1 - SCF)

SelfLiabilityRA=SelfCollateral⋅SCF=CollateralRA/(1−SCF)⋅SCFSelfLiability_{RA} = SelfCollateral \cdot SCF = Collateral_{RA} / (1 - SCF) \cdot SCF

计算此时的杠杆倍数即为 Self_Liability 和 Collateral_RA 的比值(因为只做 mint 操作，所以没有 Liablities 部分)：

LeverageMax=SelfLiability/CollateralRA=(SelfLiabilityRA⋅SBF)/CollateralRALeverageMax = {SelfLiability} / Collateral_{RA} = ({SelfLiability_{RA}} \cdot SBF) / Collateral_{RA}

化简上述等式可得：

LeverageMax=SCF∗SBF/(1−SCF)Leverage_{Max} = SCF * SBF / (1 - SCF)

代入 SCF = 0.95, SBF = 1 可得 Leverage 的最大值是 19，即为 mint 所能使用的最大杠杆倍数。

当 SBF 固定为 1 时，影响最大杠杆倍数的因素其实就是 SCF，例如当 SCF = 0.90 时，最大倍数是 9。

Algorithm Optimization of Compute Liquidity

在 #Compute Liquidity case 6 中，我们设想了用户拥有 Self_Collateral 和 Self_Liability 之后，经过一段时间累计利息的情况，由于债务的利率通常要高于抵押的利率，所以债务累计利息的增长速度总是快于抵押累计收益的增长，最终导致 Self_Collateral 不足以完全抵消 Self_Liability，多出的债务将随时间累计到 Liabilities 中。

在之前的 case 6 中，我们分别记录了 Self_Collateral 和 Self_Liability 的数量，来计算这其中的利息差值。但是这种做法在智能合约中会存在很大的问题，因为这样计算，总是会在用户 mint 或者 burn 时去修改这两个 storage 变量（昂贵的 SSTORE 操作），并且每一位用户的每一种资产都需要单独设置两个变量记录 Self_Collateral 和 Self_Liability，在实际业务中，如此操作显然是不合理的。

Euler 对此进行了算法优化，不需要为每一位用户的每一种资产单独记录两个变量，省去了频繁的 SSTORE 操作。

  1. 首先 Self_Collateral 与 Collateral 利率相同, Self_Liability 与 Liabilities 利率相同， 之所以需要把抵押资产和负债资产各分为两类，根本原因是因为他们的风险价值调整系数不同（请看上文中的调整系数列表），对 Liquidity 的影响不同
  2. 如果能排除同时 deposit 和 borrow 同一种资产的情况，则能大大简化区分 self 数量的步骤；
    • 例如用户 deposit 3000 USDC， 又 borrow 1000 USDC，如果依然保留 3000 USDC 的抵押 和 1000 USDC 的债务，将会大大增加区分 self 部分的复杂性
    • 因此 Euler 对于这种情况的处理是直接从 deposit 中扣除 borrow ，即当用户 borrow 1000 USDC 时，实际上是没有产生新的债务，而是直接减少抵押的部分，变为 2000 USDC
  3. 有了上述约束，我们在计算每种资产的 self 部分和非 self 部分时，就可以先假设该资产的所有债务都是 Self_Liability ，进而推导 Self_Collateral = Self_Collateral_RA / SCF = Self_Liability / SCF
  4. 如果推导出的 Self_Collateral 比实际该资产的抵押要大，重设为实际的抵押数量，而剩下的未抵消的 Self_Liability 应计入 Liabilities

下面是 Euler 合约中关于流动性计算的主要代码逻辑和注释：

// contracts/modules/RiskManager.sol

function computeLiquidityRaw(
    address account,
    address[]
    memory
    underlyings
)
    private view returns (LiquidityStatus memory status)
{

    ...

    // compute Liquidity every asset
    for (uint i = 0; i < underlyings.length; ++i) {
        ...

        // balance and owned are storage variables, not the latest value
        uint balance = assetStorage.users[account].balance;  // balanceOf EToken
        uint owed = assetStorage.users[account].owed;        // balanceOf DToken

        // If user has Liabilities in this asset, should compute
        // both Liabilities and collateral, otherwise, accumulate
        // collateralValue memory variable directly
        if (owed != 0) {
            ...

            // The latest balanceOf DToken,
            // often different from owed (greater)
            uint assetLiability = getCurrentOwed(
                                    assetStorage,
                                    assetCache,
                                    account
                                  );

            // self-collateralization
            // If balance of EToken is not zero,
            // means user has collateral in this asset
            if (balance != 0) {
                // User's actually collateral balance of underlying
                uint balanceInUnderlying = balanceToUnderlyingAmount(
                    assetCache, balance
                );

                // CONFIG_FACTOR_SCALE for adjusting decimals (1 in uint32)
                // SELF_COLLATERAL_FACTOR is constant value (0.95)

                // selfAmount cache Liabilities amount (Self_Collateral_RA)
                // First of all, we assume that all debt are Self_Liability,
                // then we can get Self_Collateral
                // Self_Collateral * SCF = Self_Collateral_RA = Self_Liability
                // Self_Collateral = Self_Liability / SCF
                uint selfAmount = assetLiability;
                uint selfAmountAdjusted =
                        assetLiability * CONFIG_FACTOR_SCALE / SELF_COLLATERAL_FACTOR;

                // If assetLiability > all collateral of the asset at this time,
                // this is obviously. unreasonable, indicating that the assumption
                // does not hold. So we reset Self_Collateral to balanceInUnderlying
                // and the remaining part of
                // assetLiability - balanceInUnderlying is the actual Liabilities
                if (selfAmountAdjusted > balanceInUnderlying) {
                    selfAmount = balanceInUnderlying * 
                                    SELF_COLLATERAL_FACTOR / CONFIG_FACTOR_SCALE;
                    selfAmountAdjusted = balanceInUnderlying;
                }

                {
                    // (balanceInUnderlying - selfAmountAdjusted)*BF*price is
                    // actually Collateral_RA without Self_Collateral
                    uint assetCollateral = 
                        (balanceInUnderlying - selfAmountAdjusted) *
                            config.collateralFactor /
                            CONFIG_FACTOR_SCALE;
                    assetCollateral += selfAmount;
                    // accumulate collateralValue
                    status.collateralValue += assetCollateral * price / 1e18;
                }

                // Liabilities without Self_Liabilities
                assetLiability -= selfAmount;
                status.liabilityValue += selfAmount * price / 1e18;
                ...
            }

            // accumulate debt without self-liabilities
            // this part use borrowFactor is different from
            // self_collateral_factor (constant 0.95)
            assetLiability = assetLiability * price / 1e18;
            assetLiability = config.borrowFactor != 0 ?
                assetLiability * CONFIG_FACTOR_SCALE / config.borrowFactor :
                MAX_SANE_DEBT_AMOUNT;
            status.liabilityValue += assetLiability;
        } else if (balance != 0 && config.collateralFactor != 0) {
            // owed == 0 && balance != 0
            // user only have Collateral in this asset

            ...

            // convert Etoken amount to Underlying_amount
            // collateralValue += Underlying_amount * collateralFactor
            uint balanceInUnderlying = balanceToUnderlyingAmount(assetCache, balance);
            uint assetCollateral = balanceInUnderlying * price / 1e18;
            assetCollateral =
                assetCollateral * config.collateralFactor / CONFIG_FACTOR_SCALE;
            status.collateralValue += assetCollateral;
        }
    }
}

Short

Short with Leverage

Euler 允许使用杠杆做空。假设使用 WETH 做空 UNI (ShortOn: UNI, Against: WETH)：

  1. 首先 deposit 1 WETH
  2. mint 价值 3 WETH 的 UNI，则会同时产生 3 WETH 价值的抵押和债务
  3. 其中 3 * 0.95 = 2.85 WETH 价值的 Self_Liability 被 3WETH 价值的 Self_Collateral 抵消
  4. 产生了 3 * (1 - 0.95) = 0.15 WETH 价值的 Liabilities
  5. 调用 Euler 的 swap 接口，Euler 合约会将 UNI-EToken 转换成 UNI ，然后去 UNI-WETH uniV3Pool 中兑换成等值的 WETH，最后 Euler 合约转换成 WETH-EToken 返回给用户
  6. 一段时间后，当 UNI 价格下降，用户的 UNI-DToken 债务价值下降，此时用户用 WETH-EToken 去兑换 UNI-EToken 将花费更少，剩下未兑换部分 WETH-EToken 作为做空的利润
  7. 我们先忽略这段时间借贷利息的成本和抵押的资产收益，假设 UNI-DToken 的价值由于价格下跌减小了 1%，那么用户将获利将是 3 WETH 债务的 1% ，即 0.03 WETH，相较于用户直接做空 1 WETH 的 UNI 获利 0.01 WETH，上述方式获得了 3 倍杠杆的加成

short scripts

由于 Euler 前端代码暂未开源(截止 2022 年 5 月 10 日)，我们编写了交互脚本与 Euler 合约交互，模拟使用 Euler mint 特性来使用 WETH 做空 UNI。这里使用 fork-mainnet 网络模拟交易环境。

Euler vs. Perpetual

Euler 其独有的杠杆借贷机制使得借贷协议同时具备了杠杆做多和杠杆做空的功能。那么与当前的主流永续合约 Defi 项目 Perpetual Protocol 相比如何呢？

Perptual Protocol 永续协议是基于 Uniswap V3 实现的去中心化永续合约交易协议，其实现思路是将用户的抵押资产与交易资产分隔开来，抵押资产存入 Vault 模块，而永续合约市场所交易的实际上是协议内部生成的 virtual token。

Perp v1 & v2 Architecture

如上图所示，Perp v1 和 v2 都有一个 vAMM 模块（Uniswap pool），交易对 token 都是 vToken(virtual token) ，永续合约的交易实际上就是做 vToken 的交易，而得益于 vToken 只是在协议内部流通，Perp 可以根据用户设置的杠杆倍数来 mint vToken 的数量。

Euler 与 Perpetual V2 永续合约功能的特性对比：

FeaturesEulerPerpetual V2
Max Leverage< 10X(根据 Factor 计算)10X
Trade CostBorrowing interest costFunding Payments & Swap fees
Price OracleUniswapV3 TWAPChainlink
limit order不支持未来会支持
  • 做多与做空的最大杠杆倍数
    • Perp V2 目前最大杠杆被设定为 10 倍;
    • Euler 要根据抵押资产和做空资产的 factor 计算，通常小于 10 倍 （使用前端的 Short/Long 功能）;
  • 交易成本
    • Perp V2 的交易成本除了永续合约的 Funding Payments，还有 vToken 做 Swap 时产生的交易费
    • Euler 对于永续合约交易者而言，其成本是借贷利息费用的支出；当然由于用户抵押资产有一个利息收入，另外目前 Euler 开启了流动性挖矿，借贷资产还有额外的 EUL token 奖励，计算交易成本时还需要考虑这两部分的收益，实际的交易费用支出会比较小，甚至根据 EUL 价格的波动，还可能出现无费用的情况；
  • 价格预言机（永续合约中的 Index Price）
    • Perp V2 主要使用 Chainlink 作为喂价来源（链下数据）
    • Euler 则完全依赖 Uniswap V3 pool TWAP (链上数据)
  • 永续合约的限价单功能
    • Perp V2 理论上可以实现 limit order 功能，项目方目前也在开发中
    • Euler 目前没有规划此功能

可以看出 Euler 与 Perpetual 各有优势。 Euler 虽然是基于借贷协议的框架，却凭借其独有的杠杆借贷算法机制实现了永续合约功能，是一项颇具巧思的创新。