Repegging of Curve v2 CryptoSwap

a price self-adjusted Ouroboros

Curve v2 CryptoSwap 详解系列：

1. Curve v2 CryptoSwap: white paper
2. Curve v2 CryptoSwap: add and remove liquidity
3. Curve v2 CryptoSwap: exchange and fee
4. Curve v2 CryptoSwap: repegging
5. Curve v2 CryptoSwap: math lib

从 curve v1 StableSwap 到 curve v2 CryptoSwap 最关键的改变就是增加了 repegging 机制，使得 AMM 的曲线可以根据 EMA 价格实现自我调节。当内部价格上升时，曲线更平缓，内部价格下降时，曲线更弯曲。换言之，在内部价格上升时减小交易的滑点，内部价格下降时增大交易滑点。

Repegging 会将一部分手续费利润沉淀下来成为新的流动性，使得流动性在长期来看是会不断累加的，即便不再有新的流动性增加。

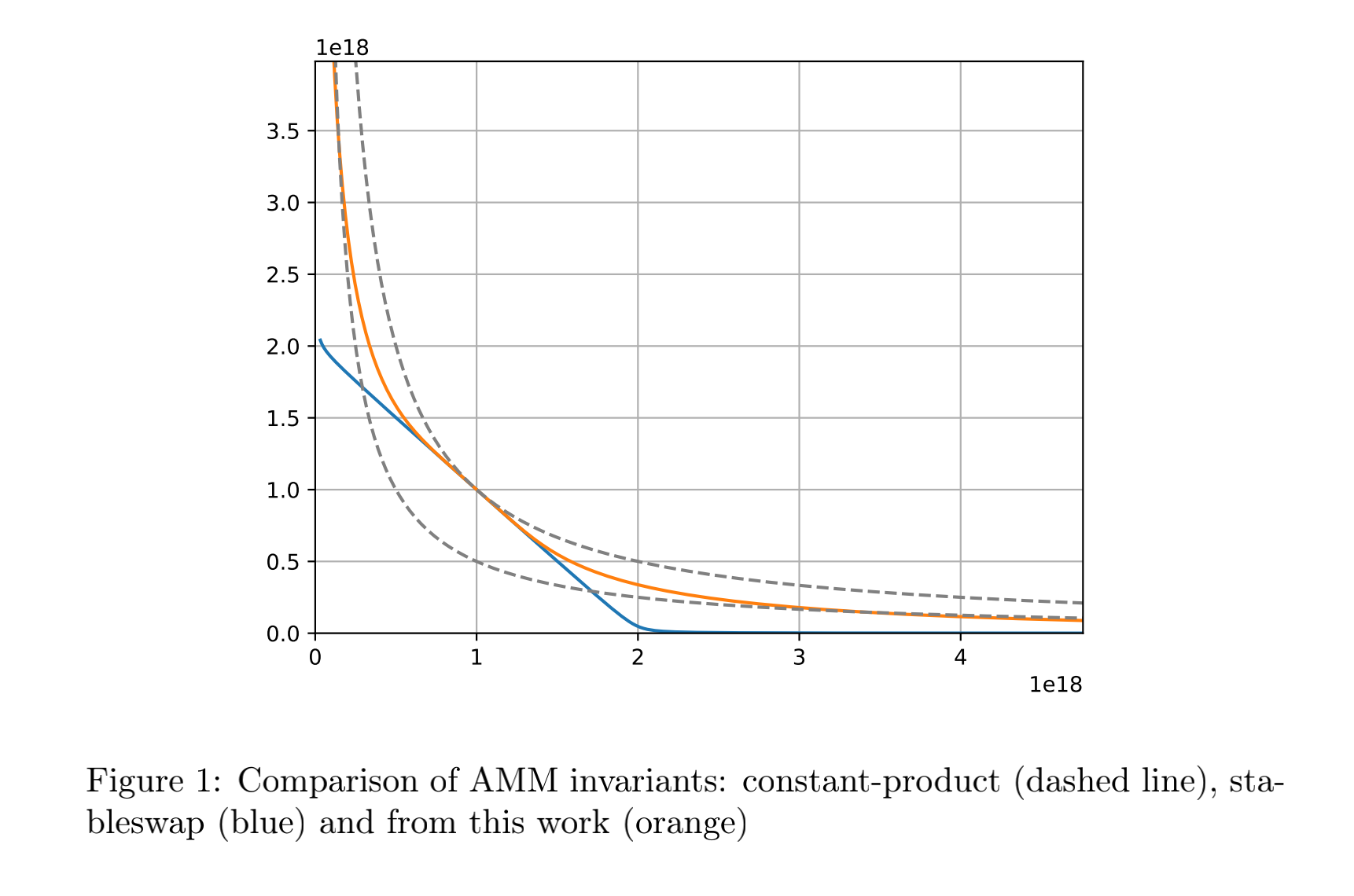
观察上图，curve v1 StableSwap （蓝色曲线）有相当大的区域曲线都是近似一条直线的，因为 v1 中的资产之间的相对价格波动很小，例如稳定币之间。近似直线的区域给予交易者的滑点是非常小的，如果把整条曲线看作一个平底锅，那么锅底的部分就是交易者的最爱。

curve v2 CryptoSwap 的曲线（橙色曲线）则是一个不那么平的平底锅，因为其资产之间的价格波动会更大，不再是如稳定币之间微小的波动。尽管如此，v2 的曲线依旧在平衡点附近具有近似直线的区域。是的，v2 依旧有交易者们最爱的锅底，只是没有 v1 那么宽而已。

Relationship of Differenet Invariants

为了更好的理解 Repegging 的逻辑，我们来梳理一下 CryptoSwap 内几个重要变量的关系。

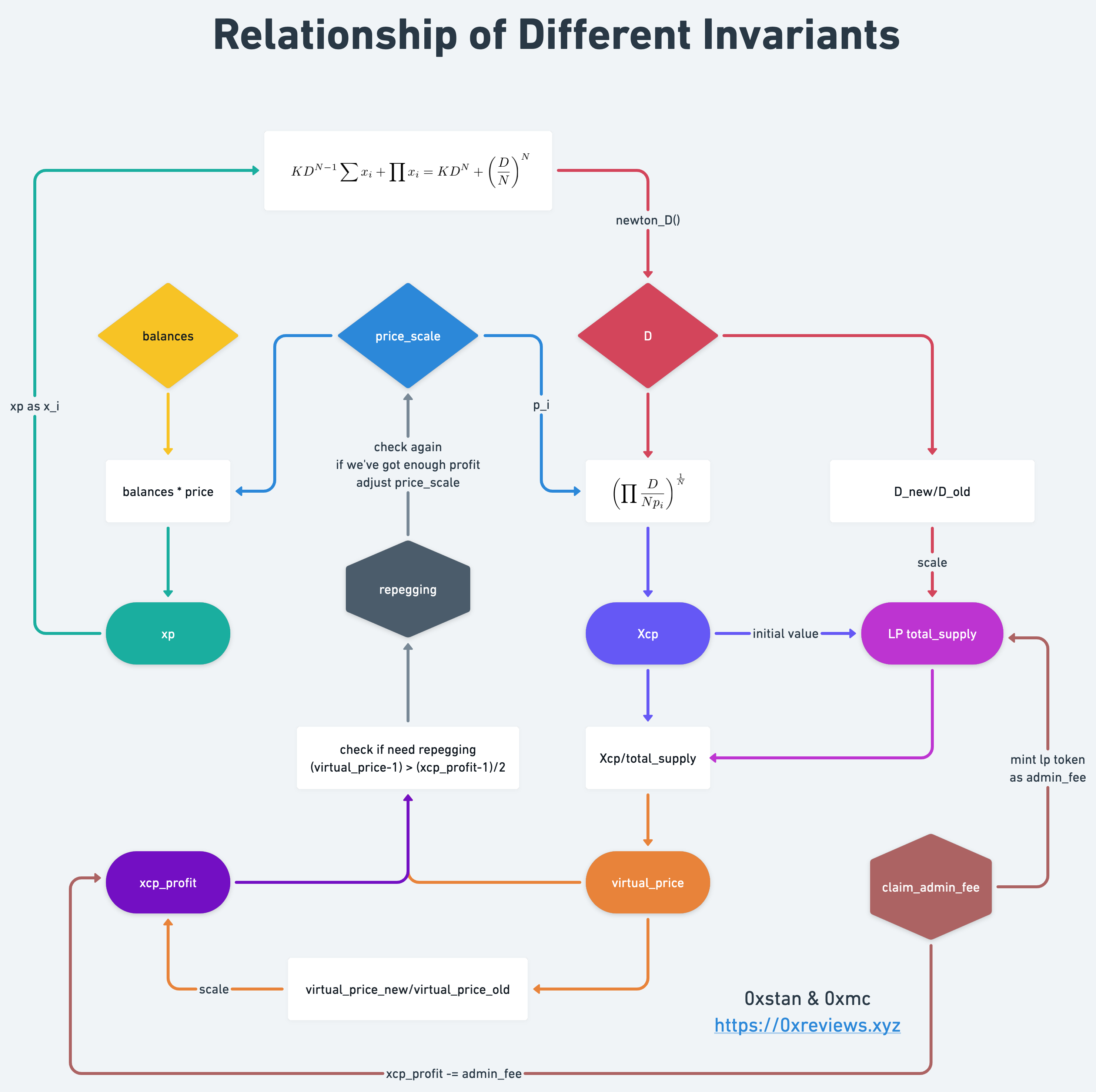
点击这里查看 Relationship of Differenet Invariants 大图

菱形是基础变量，圆角矩形是由基础变量计算得出的变量，六边形代表的是调整变量的程序逻辑，并不是变量。

首先从三个菱形的变量出发，他们是衍生出其他变量的基础变量：

• balances 池内资产的 token 数量
• price_scale 内部缩放价格，注意并不是交易时的价格
• D 即核心平衡等式中的 D

接下来由基础变量组合而成的另个圆角矩形变量，xp 与 X_cp：

• xp 是数量与价格的乘积 balances * price_scale 即价值
• X_cp 是 price_scale 和 D 经由计算公式 $X_{cp}=(\prod{\frac{D}{Np_i}})^{\frac{1}{N}}$ 计算得出的数值，用于衡量池内流动性的量化数值，我们稍后将展开解释

得出 xp 之后，我们就能代入核心平衡等式中，利用牛顿法去更新 D 的值。注意核心平衡等式中的x_i是 xp，并不是balanes。

$KD^{N-1}\sum{x_i}+\prod{x_i}=KD^N+(\frac{D}{N})^N$

LP total_supply 是 LP token 的发行总量，其值与 X_cp 和 D 有关：

• 当池子添加了第一笔流动性之后，会将 X_cp 的值作为 LP token 总发行量的初值
• 而每当 D 值改变，将会同比缩放 total_supply_new = (D_new / D_old) * total_supply_old

virtual_price 和 xcp_profit 是两种衡量每单位 LP token 所代表价值的量化数值，两者具体的区别我们在后续详细展开讨论。

X_cp

curve v2 CryptoSwap 对于 X_cp 的定义是：

$X_{cp}=(\prod{\frac{D}{Np_i}})^\frac{1}{N}$

它是对 pool 内总流动性的量化，可以当作 Uniswap 中的 L 来理解，而括号内部分则相当于 k。

以 Uniswap v2 为例，其核心公式：

$xy=k=L^2$

x 和 y 分别是资产数量，令价格处于平衡点时，资产价值(数量与价格的乘积)之和为 D，内部资产价格为 p，可以改写为：

$xy=\frac{D}{2p_x} \cdot \frac{D}{2p_y}=\prod{\frac{D}{2p_i}}=k=L^2$

因此

$L=(\prod{\frac{D}{2p_i})^{\frac{1}{2}}}$

我们将等式拓展为 N 个资产类别的情况，则：

$L=(\prod{x_i})^{\frac{1}{N}}=(\prod{\frac{D}{Np_i}})^{\frac{1}{N}}$

最终我们得出结论：

$X_{cp}=(\prod{\frac{D}{Np_i}})^\frac{1}{N}=L$

需要注意的是，只有当处于平衡点时，资产价值之和才与 D 等价，离开平衡点该关系并不成立。

我们可以把流动性看作 N 维的几何量，例如 Uniswap v2 的流动性是 xy 的乘积，即为边长为 x 和 y 的面积，x 和 y 相等时的长度即为 $X_{cp}$ (L)，是正方形的边长。而拓展到三维，流动性可以看作是立方体， $X_{cp}$ 则是正立方体的边长。

这种衡量流动性的做法，实际上就是将 N 维的量转换成一维的量，便于比较和计算，具备了线形可叠加性。

Repegging flow

repegging 的流程可以总结为三种价格内部循环调整彼此的过程，在不依赖于外部的价格预言机的情况下，调整 AMM 曲线形态。

Internal cycle adjustment

我们首先来看简化版的流程图：

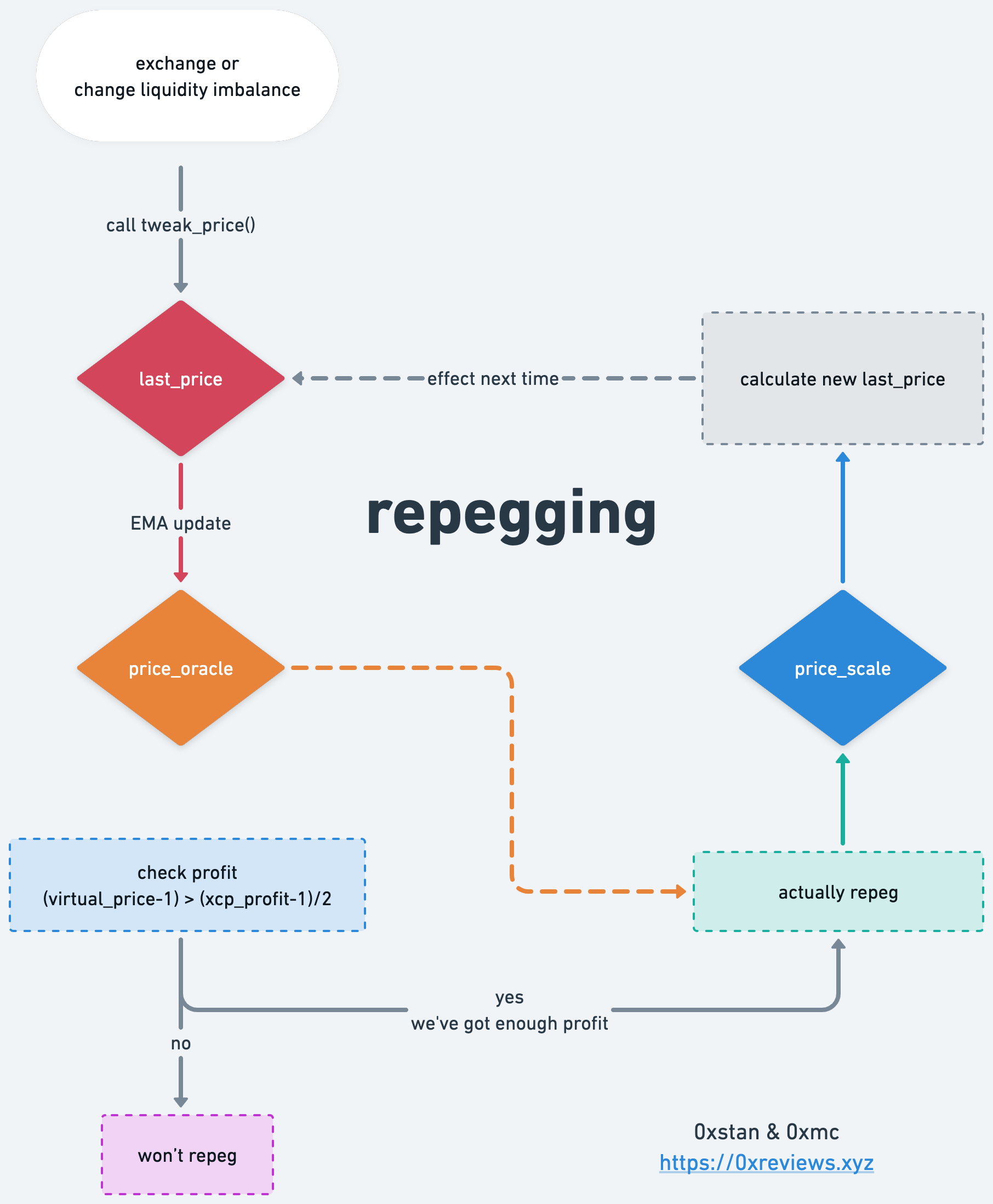
• 当一笔交易或者一笔不平衡的流动性操作触发后，会产生一个交易价格，即为 last_price。（我们认为不平衡的流动性操作过程中也发生了交易行为）
• last_price 会根据 EMA 时间加权规则更新内部预言机价格 price_oracle
• 每当积累了足够利润，使用 price_oracle 对内部缩放价格 price_scale 进行调整，即进行 repeg
• 调整后的 price_scale 又将会影响 D 的值以及后续的交易的滑点，那么下一次交易的价格 last_price 也将受到影响，至此形成了内部价格调整闭环

Repeg step by step

当然，实际程序中的流程会复杂的多，我们在简洁明了和主要逻辑的完整性之间做了取舍，尝试梳理出 repegging 的真正流程：

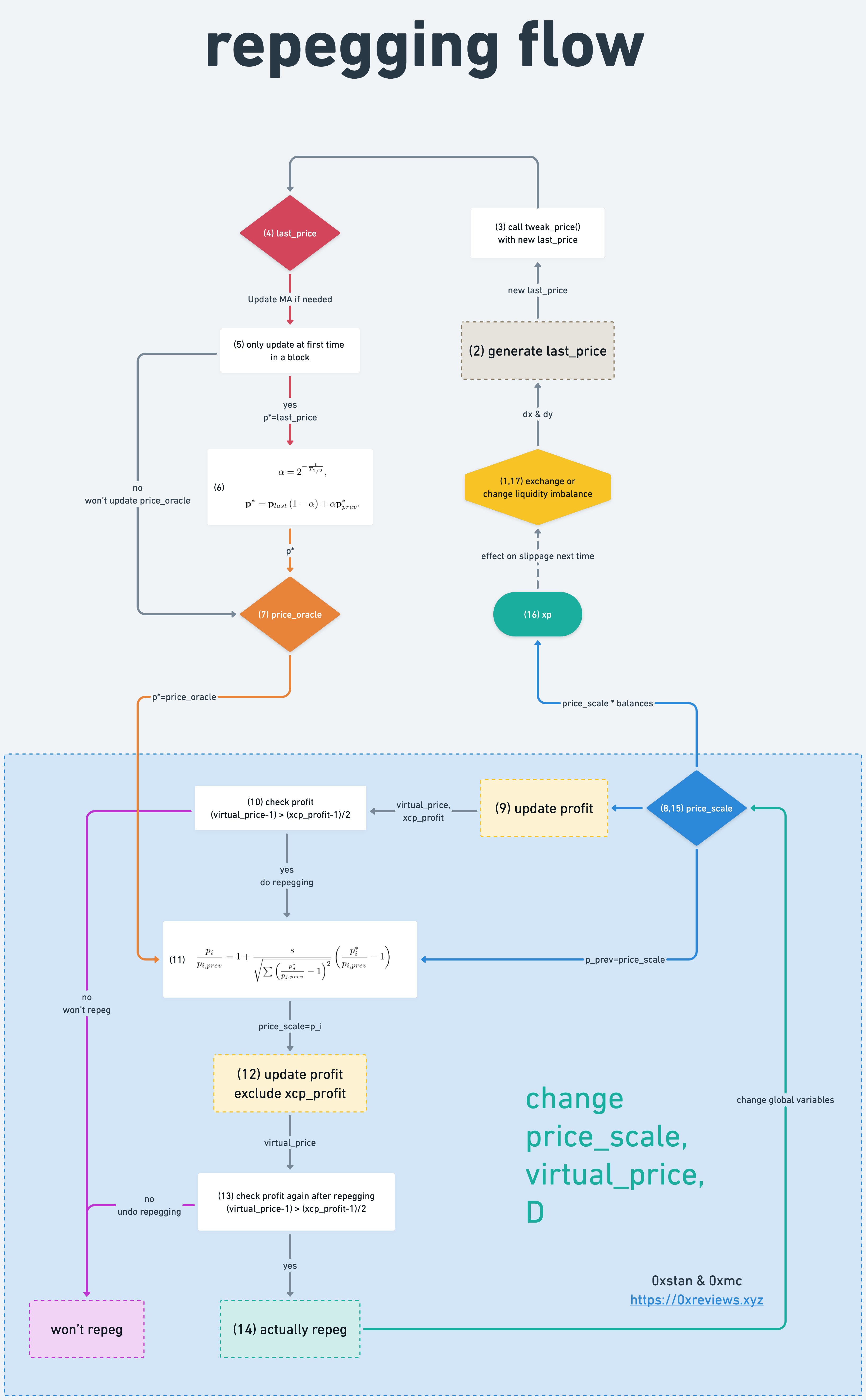
也许你需要点击放大仔细查看，这里因为版面原因，图片被缩小了。点击这里查看 repegging-flow 大图

为了方便描述，我们在图中标出了每一步的序号，有些圆括号内存在多个以逗号分隔的序号，说明流程会重复走到此处。

接下来让我们一起踏上 repegging 的旅程吧！

Trigger phase

(1) - (7) 是触发阶段，将会更新交易最新价格 last_price 和 内部预言机价格 price_oracle，为 repegging 的核心逻辑做准备。

(1) 图中黄色六边形，当一笔交易或者一笔不平衡的流动性操作触发后，会产生交易的输入和输出价值 dx 与 dy，需要注意的是，触发 repeg 的交易不会受到当前 repeg 的影响，换言之 repeg 只会影响之后的交易。

exchange(), add_liquidity(), remove_liquidity_one_coin() 三个函数都会触发 repegging 逻辑，其中关于流动性的操作，只有当增加或移除的流动性价值不平衡时，才会触发。

# tricrypto/CurveCryptoSwap.vy

@payable
@external
@nonreentrant('lock')
def exchange(i: uint256, j: uint256, dx: uint256, min_dy: uint256, use_eth: bool = False) -> uint256:
    # A and gamma are part of K, the coiffient of core invariant formula
    A_gamma: uint256[2] = self._A_gamma()
    # xp, for now put balances in it first, will multiply price_scale later
    xp: uint256[N_COINS] = self.balances
    # j is the index of output token
    ix: uint256 = j
    ...

    # Calculate price with dx and dy
    # xp will be updated by dx and dy
    # ix is the index of output token
    # p is the price of this trade, maybe dy/dx or dx/dy, according to the i and j
    # new_D is 0 means need calculate D's value in tweak_price() by newton_D()

    # when a trade complete, will call tweak_price()
    self.tweak_price(A_gamma, xp, ix, p, 0)


@external
@nonreentrant('lock')
def add_liquidity(amounts: uint256[N_COINS], min_mint_amount: uint256):
    ...

    # only call tweak_price() when add liquidity imbalanced
    # exclude first addition of the pool
    if old_D > 0:
        ...
        self.tweak_price(A_gamma, xp, ix, p, D)
    else:
        ...

@external
@nonreentrant('lock')
def remove_liquidity(_amount: uint256, min_amounts: uint256[N_COINS]):
    ...
    # won't call tweak_price here, because it's remove liquidity balanced.

@external
@nonreentrant('lock')
def remove_liquidity_one_coin(token_amount: uint256, i: uint256, min_amount: uint256):
    ...
    # call tweak_price here, because it's remove liquidity imbalanced.
    self.tweak_price(A_gamma, xp, i, p, D)

接下来是根据 dx, dy 计算出 (4) last_price，使用时间加权规则更新 (7) price_oracle

• (2) 根据交易产生的 dx, dy 生成最新的交易价格
  • 具体细节参见 # Generate last_price
• (3) 使用最新的交易价格作为入参，调用 tweak_price() 函数，进入 repegging 逻辑
• (4) 将最新的交易价格赋值给 last_price
• (5) 如果有必要，使用 last_price 更新内部预言机价格 (7) price_oracle
  • 预言机价格的更新只会发生在每个区块的第一笔交易中，即每个区块最多一次，如果区块内有多笔交易，将只会在第一笔交易中更新，忽略后续的交易
  • (6) 根据 EMA 预言机价格的更新公式计算新的内部预言机价格

oracle.1: $\alpha=2^{-\frac{t}{T_{1/2}}}$

oracle.2: $p^*=p_{last}(1-\alpha)+\alpha p^*_{prev}$

# tricrypto/CurveCryptoSwap.vy

@internal
def tweak_price(A_gamma: uint256[2], _xp: uint256[N_COINS],
                  i: uint256, p_i: uint256, new_D: uint256):
    # init prices containers
    price_oracle: uint256[N_COINS-1] = empty(uint256[N_COINS-1])
    last_prices: uint256[N_COINS-1] = empty(uint256[N_COINS-1])
    price_scale: uint256[N_COINS-1] = empty(uint256[N_COINS-1])

    # Update MA if needed
    # the two for-loops below split packed structure data into array
    # self.price_oracle_packed -> price_oracle
    # self.last_prices_packed -> last_prices
    packed_prices: uint256 = self.price_oracle_packed
    for k in range(N_COINS-1):
        price_oracle[k] = bitwise_and(packed_prices, PRICE_MASK)  # * PRICE_PRECISION_MUL
        packed_prices = shift(packed_prices, -PRICE_SIZE)

    last_prices_timestamp: uint256 = self.last_prices_timestamp
    packed_prices = self.last_prices_packed
    for k in range(N_COINS-1):
        last_prices[k] = bitwise_and(packed_prices, PRICE_MASK)   # * PRICE_PRECISION_MUL
        packed_prices = shift(packed_prices, -PRICE_SIZE)

    # Update only once at most in a block.
    if last_prices_timestamp < block.timestamp:
        # MA update required
        ma_half_time: uint256 = self.ma_half_time # T_1/2 of formula oracle.1
        # alpha of formula oracle.1
        alpha: uint256 = Math(math).halfpow((block.timestamp - last_prices_timestamp) * 10**18 / ma_half_time, 10**10)
        packed_prices = 0  # clear prices container for cache price_oracle
        # update price_oracle by formula oracle.2
        for k in range(N_COINS-1):
            price_oracle[k] = (last_prices[k] * (10**18 - alpha) + price_oracle[k] * alpha) / 10**18
        for k in range(N_COINS-1):
            packed_prices = shift(packed_prices, PRICE_SIZE)
            p: uint256 = price_oracle[N_COINS-2 - k]  # / PRICE_PRECISION_MUL
            assert p < PRICE_MASK
            packed_prices = bitwise_or(p, packed_prices)
        self.price_oracle_packed = packed_prices      # store prices to packed
        self.last_prices_timestamp = block.timestamp  # update timestamp

    ...

Core of repegging

(8) - (15) 是 repegging 的核心逻辑（图中蓝色区域）。从 (8) 调整前的 price_scale 到 (15) 调整后的 price_scale，完成了对 price_scale, virtual_price, xcp_profit, D 值的调整（全局变量的更新）。

• (9) update profit 是根据内部缩放价格 (8) price_scale 计算出 virtual_price 和 xcp_profit 的过程
  • 详见 # Update profit
• (10) 检查当前是否积累了足够的利润，可以触发 repegging
  • (vritual_price - 1) > (xcp_profit - 1)/2 满足该条件才能继续进行 repeg，否则将不会执行调整逻辑
  • 关于检查条件的意义详见 # Condition of undo price adjustment
  • 实际代码中，第一次条件检查还增加了一个阈值 allowed_extra_profit，目的是为了避免在临界点附近，频繁的触发 repegging 条件检查
  • 即 (virtual_price-1) > (xcp_profit-1)/2 + allowed_extra_profit
  • 目前线上合约参数将 allowed_extra_profit 都设定的非常小，几乎可以忽略不计，所以这个阈值目前对 repegging 过程没有影响
  • 2022 年 4 月 2 日 tricrypto2 的 allowed_extra_profit 参数值为 2*10**12，相对于量化利润的精度 10**18 是非常小的数值
• (11) 根据公式以内部预言机价格计算出调整后的 price_scale
  • 其中 $p_{i,prev}$ 和 $p_{j,prev}$ 是调整之前的 (8) price_scale 数值，$p_i^*$ 是 (7) price_oracle，而 $p_i$ 则是我们需要求的调整之后的 price_scale
• (12) update profit 使用调整后的 price_scale 第二次进行量化利润的更新，注意这一次不会更新 xcp_profit
  • 因为量化利润的计算都是基于 price_scale 所以当内部缩放价格发生改变，相应的量化利润也需要更新
  • 本次对量化利润的更新将不包括 xcp_profit ，我们等会再来展开讨论其中的原因
• (13) 在更新量化利润之后，第二次检查 repegging 条件，如果调整之后的 price_scale 不再满足条件，则不进行实际的 repeg 调整
  • 第二次 repeg 条件检查没有添加阈值 allowed_extra_profit，因为第一次已经做了防止频繁触发的处理
  • 如果不满足条件，则流程结束，因为调整后的 price_scale 数值只存于缓存中的变量，并没有真正赋值给 storage 中的全局变量，所以当 tweak_price() 函数运行完成，缓存中的变量将被销毁，相当于撤销了对 price_scale 的调整，即白皮书中描述的 "undo p adjustment"
• (14) 真正执行 repegging ，将调整后的内部价格赋值给全局变量
• (15) price_scale 即改变后的全局变量 self.price_scale_packed

$\frac{p_i}{p_{i,prev}}=1+\frac{s}{\sqrt{\sum{(\frac{p_j^*}{p_{j,prev}}-1)^2}}}(\frac{p_i^*}{p_{i,prev}}-1)$

上述公式是使用 price_oracle 更新 price_scale 的公式，我们稍作变形便于接下来的理解：

$\frac{p_i}{p_{i,prev}}-1=\frac{s}{\sqrt{\sum{(\frac{p_j^*}{p_{j,prev}}-1)^2}}}(\frac{p_i^*}{p_{i,prev}}-1)$

1. 调整的思路是在每次交易后，让 price_scale 向 price_oracle 做一定程度的偏移
2. 构建一个 N 维的向量空位(N 是资产数量)，我们可以将变化前后的价格的比值 $\frac{p_i}{p_{i,prev}}$ 组成的数组作为其中的向量，那么 1 即为坐标系的原点
3. 将更新前后的价格的比值作为比较对象
   • $\frac{p_i}{p_{i,prev}}-1$ price_scale 的前后比值
   • $\frac{p_i^*}{p_{i,prev}}-1$ price_oracle 和 price_scale 的比值
   • 比值 - 1 实际上就是计算到向量和原点 1 的差值
4. $\frac{s}{\sqrt{\sum{(\frac{p_j^*}{p_{j,prev}}-1)^2}}}$
   • s 是 step 的缩写，即调整步长；
   • 分母可以理解为向量到原点的距离（各个维度与原点的平方差）
5. 最后根据这个调整系数来让 price_scale 向 price_oracle 靠拢

其中代码对应公式中的项：

• p_new: $p_i$
• price_scale: $p_{i,prev}$
• price_oracle: $p^*_j$
• adjustment_step: s
• ratio: $\frac{p_j^*}{p_{j,prev}}-1$
• norm: $\sqrt{\sum(\frac{p_j^*}{p_{j,prev}}-1)^2}$

# tweak_price()

# Update profit numbers without price adjustment first
...

needs_adjustment: bool = self.not_adjusted

# check profit first time
# if not needs_adjustment and (virtual_price-10**18 > (xcp_profit-10**18)/2 + self.allowed_extra_profit):
# (re-arrange for gas efficiency)
if not needs_adjustment and (virtual_price * 2 - 10**18 > xcp_profit + 2*self.allowed_extra_profit):
    needs_adjustment = True
    self.not_adjusted = True

if needs_adjustment:
    adjustment_step: uint256 = self.adjustment_step  # s of formula
    norm: uint256 = 0

    # calculate norm
    for k in range(N_COINS-1):
        ratio: uint256 = price_oracle[k] * 10**18 / price_scale[k]
        if ratio > 10**18:
            ratio -= 10**18
        else:
            ratio = 10**18 - ratio
        norm += ratio**2

    # if norm <= s**2 means s/sqrt(norm) > 1 , will change too much
    # that's not allowed.
    # virtual_price is 0 means it hasn't inited
    if norm > adjustment_step ** 2 and old_virtual_price > 0:
        norm = Math(math).sqrt_int(norm / 10**18)  # Need to convert to 1e18 units!

        # update every p_new by formula, exclude coin[0]
        for k in range(N_COINS-1):
            p_new[k] = (price_scale[k] * (norm - adjustment_step) + adjustment_step * price_oracle[k]) / norm

        # Calculate balances*prices
        xp = _xp
        for k in range(N_COINS-1):
            xp[k+1] = _xp[k+1] * p_new[k] / price_scale[k]

        # Calculate "extended constant product" invariant xCP and virtual price
        D: uint256 = Math(math).newton_D(A_gamma[0], A_gamma[1], xp)
        xp[0] = D / N_COINS
        for k in range(N_COINS-1):
            xp[k+1] = D * 10**18 / (N_COINS * p_new[k])
        # @notice: We reuse old_virtual_price here but it's not old anymore
        old_virtual_price = 10**18 * Math(math).geometric_mean(xp) / total_supply

        # check profit senond time
        # Proceed if we've got enough profit
        # if (old_virtual_price > 10**18) and (2 * (old_virtual_price - 10**18) > xcp_profit - 10**18):
        if (old_virtual_price > 10**18) and (2 * old_virtual_price - 10**18 > xcp_profit):
            packed_prices = 0
            for k in range(N_COINS-1):
                packed_prices = shift(packed_prices, PRICE_SIZE)
                p: uint256 = p_new[N_COINS-2 - k]  # / PRICE_PRECISION_MUL
                assert p < PRICE_MASK
                packed_prices = bitwise_or(p, packed_prices)
            self.price_scale_packed = packed_prices
            self.D = D
            self.virtual_price = old_virtual_price

            return

        else:
            self.not_adjusted = False

Tail of ouroboros

(16) - (17) 衔尾蛇的尾巴 —— repegging 对于后续交易产生的影响，CryptoSwap 内部价格调整机制形成的闭环。

如前文所述，reppegging 不会影响当时的交易，但是由于改变了内部缩放价格 price_scale 所以会对后续的交易产生影响。即 (1) 触发 repegging 所使用的 (4) last_price 是由 (1) 之前的 repegging 决定的，而这一轮 repegging 产生的 (15) last_price 将提供给下一轮交易 (17) 的 repegging。

• (16) xp 由被 repegging 调整过的内部缩放价格 (15) price_scale 和 balances 的乘积计算出新的 xp 值
• 新的 xp 值将会影响后续交易的 newton_y() 的计算
• (17) 一笔新的交易或者不平衡的流动习操作将会触发新一轮的 repegging, the beginning of another story ...

Generate last_price

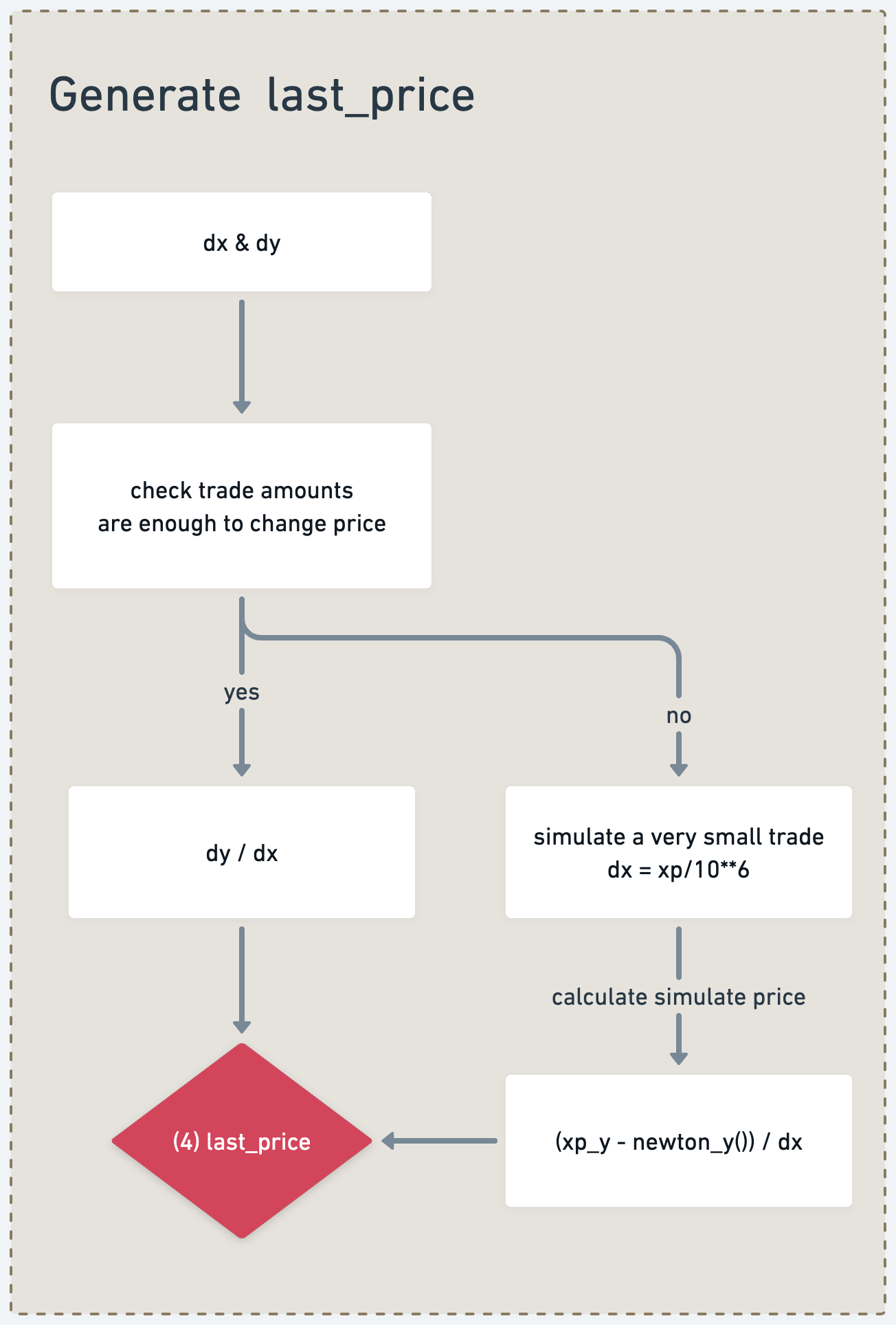
• 根据交易量分两种情况计算新的交易价格 p_new
  • 如果交易量足够大，dx > 10**5 and dy > 10**5，对下一次的交易价格产生较大影响（滑点变化较大），将直接计算最新的交易价格 p_new = dy/dx
  • 如果交易量很小，dx 和 dy 都小于 10**5，那么将以现有 xp[0] 值的百万分之一作为输入量，模拟一笔极小量的交易 dx = xp/10**6
  • 将 newton_y() 计算结果和现有 xp 的差作为交易输出量，与输入量的比值即为新的交易价格 p_new = (xp_y - newton_y()) / dx
• (4) last_price 就是被更新后的最新交易价格，它将被用于下一轮 repegging 的计算

@payable
@external
@nonreentrant('lock')
def exchange(i: uint256, j: uint256, dx: uint256, min_dy: uint256, use_eth: bool = False) -> uint256:
    ...

    # Calculate price when dx and dy both big enough.
    if dx > 10**5 and dy > 10**5:
        _dx: uint256 = dx * prec_i  # unite dx and dy to 10**18
        _dy: uint256 = dy * prec_j

        # because coin[0] price is always 1, we consider three cases
        # when i and j both not 0, should convert input token to coin[0],
        # because we haven't price of coin[1]-coin[2]
        # when i equls 0 is dx / dy
        # when j equls 0 is dy / dx
        if i != 0 and j != 0:
            p = bitwise_and(
                shift(self.last_prices_packed, -PRICE_SIZE * convert(i-1, int256)),
                PRICE_MASK
            ) * _dx / _dy  # * PRICE_PRECISION_MUL
        elif i == 0:
            p = _dx * 10**18 / _dy
        else:  # j == 0
            p = _dy * 10**18 / _dx
            ix = i

    # p as input param
    self.tweak_price(A_gamma, xp, ix, p, 0)


@external
@nonreentrant('lock')
def add_liquidity(amounts: uint256[N_COINS], min_mint_amount: uint256):
    ...

    # Calculate price
    # p_i * (dx_i - dtoken / token_supply * xx_i) = sum{k!=i}(p_k * (dtoken / token_supply * xx_k - dx_k))
    # Only ix is nonzero
    p: uint256 = 0
    # d_token > 10**5 means volume is big enough
    if d_token > 10**5:
        # ix < N means only add liquidity with one coin,
        # could calculate price directly.
        # otherwise need calculate price in tweak_price().
        if ix < N_COINS:
            ...
            S = S * d_token / token_supply
            p = S * PRECISION / (amounts[ix] * precisions[ix] - d_token * xx[ix] * precisions[ix] / token_supply)

    self.tweak_price(A_gamma, xp, ix, p, D)


@internal
def tweak_price(A_gamma: uint256[2], _xp: uint256[N_COINS],
                  i: uint256, p_i: uint256, new_D: uint256):
    ...

    # if p_i > 0 means price has beeb calculated before
    # otherwise (p_i == 0) means the need calculate price here,
    # need simulate a small trade to calculate price here.
    if p_i > 0:
        # Save the last price directly when i > 0 (not coin[0])
        if i > 0:
            last_prices[i-1] = p_i
        else:
            # If 0th price changed - change all prices instead
            for k in range(N_COINS-1):
                last_prices[k] = last_prices[k] * 10**18 / p_i
    else:
        # When p_i = 0, we need calcute price hrere.
        # Simulate a very small trade, input is coin[0],
        # calculate price of other two coin.
        # Use xp[0] / 10**6 as dx, that's a quite small volume.
        __xp: uint256[N_COINS] = _xp
        dx_price: uint256 = __xp[0] / 10**6
        __xp[0] += dx_price
        for k in range(N_COINS-1):
            last_prices[k] = price_scale[k] * dx_price / (_xp[k+1] - Math(math).newton_y(A_gamma[0], A_gamma[1], __xp, D_unadjusted, k+1))

    # clear prices container, store last_price to storage.
    packed_prices = 0
    for k in range(N_COINS-1):
        packed_prices = shift(packed_prices, PRICE_SIZE)
        p: uint256 = last_prices[N_COINS-2 - k]  # / PRICE_PRECISION_MUL
        assert p < PRICE_MASK
        packed_prices = bitwise_or(p, packed_prices)
    self.last_prices_packed = packed_prices

Update profit

Repegging 流程中会有两次更新 profit 的过程，以当前 price_scale 依次更新 X_cp, virtual_price, xcp_profit 的数值。

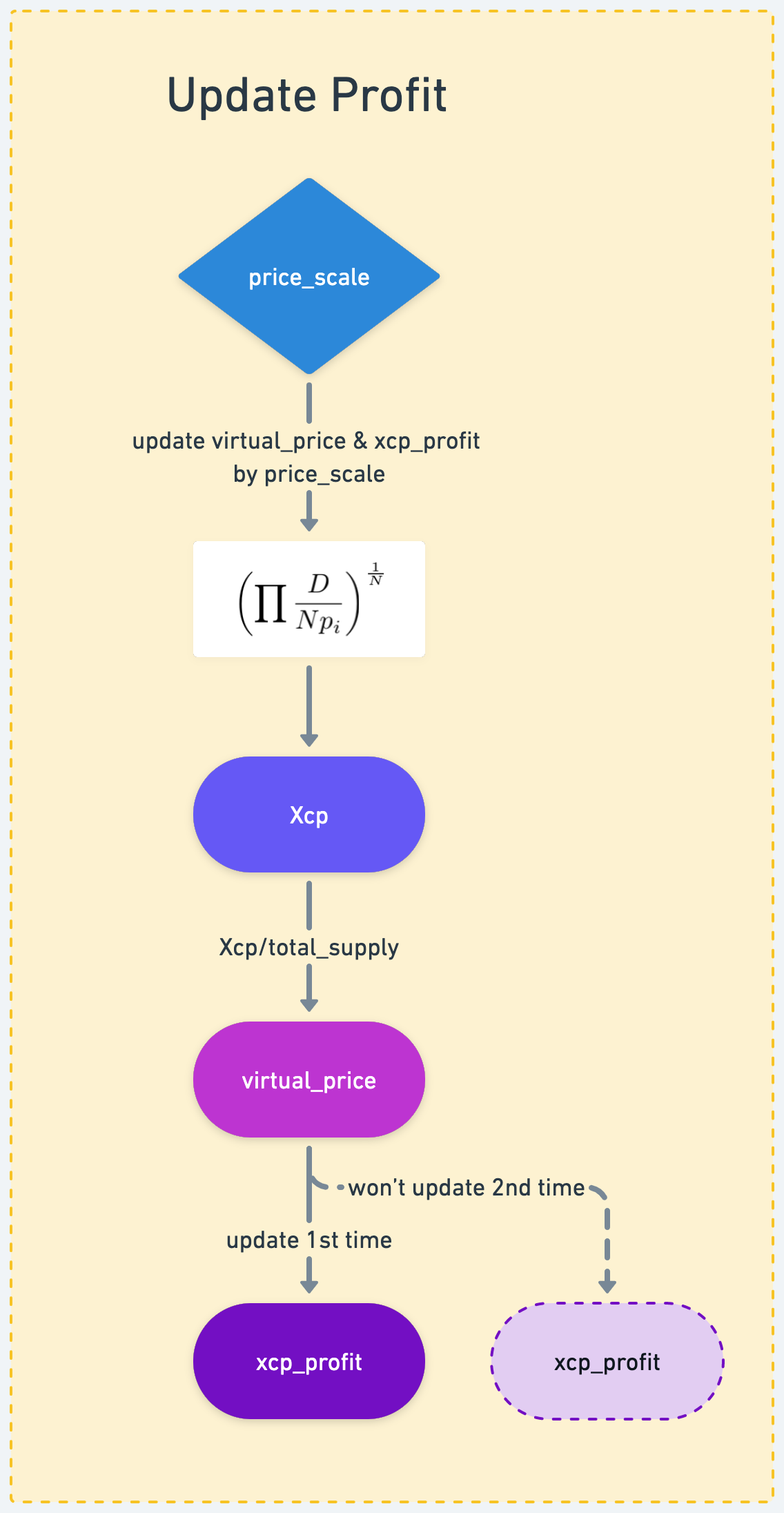
• 利用公式更新 X_cp: $X_{cp}=(\prod{\frac{D}{Np_i}})^{\frac{1}{N}}$
  • 其中 p_i 即为内部缩放价格 price_scale
• virtual_price = X_cp/total_supply
  • total_supply 是 LP token 的总发行量
  • X_cp 是对 pool 内总流动性的量化，所以 virtual_price 是衡量每单位 LP token 所代表的 流动性 + 利润
• 根据 virtual_price 的变化，同比更新 xcp_profit
  • xcp_profit = (virtual_price_new/virtual_price_old) * xcp_profit_old
  • 注意xcp_profit的更新只发生在第一次，第二次不会更新

第一次 update profit， 其中 virtual_price 必须比上次大，因为每次调用 tweak_price() 都发生了交易（包括不平衡的操作流动性），此时必定从用户那里扣除了手续费作为 pool 的利润，那么衡量每单位 LP 利润的 virtual_price 也必定增长，否则肯定发生了某些错误（例如被攻击），交易回滚。

而第二次 profit 检查则不需要该限制，因为 repegging 有可能使 virtual_price 减小。

# tweak_price()
...

total_supply: uint256 = CurveToken(token).totalSupply()
old_xcp_profit: uint256 = self.xcp_profit
old_virtual_price: uint256 = self.virtual_price

# Update profit numbers without price adjustment first

# @notice: xp here is D/(N*p_i) in formula X_cp, not xp = balance * price_scale
# coin[0]'s price is always 1, so we can omit price_scale[0]
xp[0] = D_unadjusted / N_COINS
# other coin need consider price_scale
for k in range(N_COINS-1):
    xp[k+1] = D_unadjusted * 10**18 / (N_COINS * price_scale[k])
# init xcp_profit and virtual_price with 1
xcp_profit: uint256 = 10**18
virtual_price: uint256 = 10**18

# old_virtual_price > 0 means it has inited
if old_virtual_price > 0:
    xcp: uint256 = Math(math).geometric_mean(xp)  # calculate (xp)**(1/N)
    virtual_price = 10**18 * xcp / total_supply   # need mutiply 10**18 first to make virtual_price still be 10**18
    # Scale xcp_profit by new_virtual_price / old_virtual_price
    xcp_profit = old_xcp_profit * virtual_price / old_virtual_price

    # New virtual_price must bigger than old virtual_price, otherwise revert.
    # Because every time call tweak_price(), we've got fees as profit,
    # so virtual_price must grow.
    if virtual_price < old_virtual_price and t == 0:
        raise "Loss"

self.xcp_profit = xcp_profit   # store value to storage

...

第二次 update profit，注意不会更新 xcp_profit，具体原因参见 # Difference between virtual_price and xcp_profit

# tweak_price()
...

# Update profit member senond time, after repegging.
# @notice: We reuse old_virtual_price here but it's not old anymore
# xp is D/(N*p_i) and the p_i here has been changed by repeg
old_virtual_price = 10**18 * Math(math).geometric_mean(xp) / total_supply

# Proceed if we've got enough profit
# update price_scale, D, virtual_price
# @notice: we don't update xcp_profit here, for saving gas
# if (old_virtual_price > 10**18) and (2 * (old_virtual_price - 10**18) > xcp_profit - 10**18):
if (old_virtual_price > 10**18) and (2 * old_virtual_price - 10**18 > xcp_profit):
    packed_prices = 0
    for k in range(N_COINS-1):
        packed_prices = shift(packed_prices, PRICE_SIZE)
        p: uint256 = p_new[N_COINS-2 - k]  # / PRICE_PRECISION_MUL
        assert p < PRICE_MASK
        packed_prices = bitwise_or(p, packed_prices)
    self.price_scale_packed = packed_prices
    self.D = D
    self.virtual_price = old_virtual_price

    return

Difference between virtual_price and xcp_profit

根据白皮书描述 vritual_price 就是 xcp_profit_real，即对于 liquidity provider 来说，每单位 LP token 实际可提取的收益利润的量化（不包含用于 repegging 部分的利润），而 xcp_profit 则是包含了用于 repegging 部分，总的累计利润的量化。

We also have a variable xcp_profit_real which keeps track of all losses after p adjustments. -- 《Automatic market-making with dynamic peg》

• 两者都是一种比值关系，初值都设为 10**18 (精度 18 的数值 1)
• virtual_price 总是等于 X_cp / total_supply
  • 因为 total_supply 的初值是 X_cp 所以他们的比值 virtual_price 的初值也是 1
  • 流动性的增减 与 price_scale 的改变，都会影响 D , X_cp , total_supply，最终传导到 virtual_price
• xcp_profit 由 virtual_price 同比缩放更新
  • 即 xcp_profit = (virtual_price_new / virtual_price_old) * xcp_profit_old

如果我们查看线上数据，会发现 virtual_price 与 xcp_profit 的值总是不同，后者往往比前者大，且 virtual_price - 1 总是接近于 xcp_profit - 1 的一半。

例如 2022 年 4 月 8 日， tricrypto2 pool 的数据：

• virtual_price 是 1009978512346580355
• xcp_profit 是 1019956287464410995
• virtual_price - 10**18 是 9978512346580355
• xcp_profit - 10**18 是 19956287464410995
• (virtual_price - 1)/(xcp_profit - 1) 即 9978512346580355/19956287464410995 = 0.5000184711，是近似一半的关系

为何如此？

我们可以简化一下问题，假设一个池子，进行了数笔交易，还从未发生过 repegging ，且没有调用过 claim_admin_fee() 函数，那么两者的值应该是相同的。因为两者初值都是 1，virtual_price 的变化将同比缩放 xcp_profit，此时他们的值是同步的。

直到发生了第一次 repegging，两者的值将开始不同。

让我们来回顾一下几个重要变量之间的关系：

• repegging 会改变 price_scale
• xp = balances*price_scale 也会改变
• D 也会发生改变（通过牛顿法求解）
• 进而会改变 X_cp ，因为 $(\frac{D}{Np_i})^{\frac{1}{N}}$ 包含 D 和价格 p
• 最终会传导到 virtual_price ，导致其值发生改变

而两者值的不同在于 tweak_price() 对 virtual_price 有两次更新操作 (两次 update profit)，第一次是不考虑 repeg 的情况下同时更新 virtual_price和 xcp_profit ，第二次是如果发生了 repeg 则只对 virtual_price 更新，不对 xcp_profit 更新。这导致了当下一次进入 tweak_price() 逻辑时，使用 virtual_price 对 xcp_profit 进行缩放时，将不包含 repeg 的影响。

我们来模拟两者数值在程序中的变化：

• 假设，此时 virtual_price 和 xcp_profit 数值都是 1.1。
• 第一笔交易手续费的增加，让两者数值同时增长到了 1.3
• 由于触发了 repegging，使得 virtual_price 由 1.3 被调整为 1.2，注意 repegging 不会对 xcp_profit 产生影响，所以其值仍然是 1.3
• 而紧接着第二笔交易又增加了一些利润， 让 virtual_price 从 1.2 升回到 1.3，然后对 xcp_profit 同比放大时，两者的值就开始产生分歧了
  • xcp_profit = 1.3 * 1.3 / 1.2 = 1.408333

# Fist exchange call tweak_price():
...

# Both are 1.1 at first exchange begin.
old_xcp_profit: uint256 = self.xcp_profit        # 1.1 * 10**18
old_virtual_price: uint256 = self.virtual_price  # 1.1 * 10**18

# Update both virtual_price and xcp_profit
# Suppose their value both increases to 1.3
xcp: uint256 = Math(math).geometric_mean(xp)
virtual_price = 10**18 * xcp / total_supply                       # 1.3 * 10**18
xcp_profit = old_xcp_profit * virtual_price / old_virtual_price   # 1.3 * 10**18
self.xcp_profit = xcp_profit

...

# This time we've got enough profit, do repeg.
# We reuse old_virtual_price here but it's not old anymore.
old_virtual_price = 10**18 * Math(math).geometric_mean(xp) / total_supply
self.virtual_price = old_virtual_price      # Suppose virtual_price change to 1.2 after repegging
# @notice: repeg won't change self.xcp_profit here!

...

# Second exchange call tweak_price():

# Load value that updated in first trade
old_xcp_profit: uint256 = self.xcp_profit        # 1.3 * 10**18
old_virtual_price: uint256 = self.virtual_price  # 1.2 * 10**18

# Update both virtual_price and xcp_profit
# Suppose virtual_price increases to 1.3
xcp: uint256 = Math(math).geometric_mean(xp)
virtual_price = 10**18 * xcp / total_supply                       # 1.3 * 10**18
# @important: This line very important, their values start to differ
# xcp_profit = 1.3 * 1.3 / 1.2 = 1.408333
xcp_profit = old_xcp_profit * virtual_price / old_virtual_price   # 1.408333 * 10**18

...

上述伪代码描述的是 repeg 让 virtual_price 减少的情况，当然也存在使其增大的情况，但是总的来说减少的情况居多，所以造成了 xcp_profit 的值总是比 virtual_price 要大。

Condition of undo price adjustment

也许你已经注意到了，(vritual_price - 1) > (xcp_profit - 1)/2 这个判断条件出现了两次，它就是判断 repegging 是否需要真正执行的条件（白皮书中的描述是，如果前者小于后者则会撤销 repeg 操作，与实际合约代码正好相反，但最终会得到同样的结果）。

We undo p adjustment if it causes xcp_profit_real-1 to fall lower than half of xcp_profit-1. -- 《Automatic market-making with dynamic peg》

这个条件的含义是：我们将 pool 累积总利润的一半用于repeg

virtual_price - 1 是衡量 LP 用户可得的利润，而 xcp_profit - 1 是 pool 累积的总利润（没有受到 repegging 影响）。一旦 LP 用户的手续费利润超过了累积总利润的一半，就会触发 repeg，修改 price_scale，更改 AMM 的曲线形态，将超出的利润部分作为新的流动性参与到之后的做市中。

需要注意的是 条件检查一共有2次，第一次是触发 repeg，在repeg完成后，需要再次检查，保证修改之后是否仍然满足该条件。

第二次检查的原因是因为，如果 repeg 之后 virtual_price - 1 不再大于 xcp_profit - 1 的一半，我们实际上是多挪用了 LP 的利润去做repeg，这样是不合理的。

这个条件也正好能解释 CryptoSwap 线上数据，vritual_price - 1 与 xcp_profit - 1 经常是近似一半的关系。

Claim admin fees

vritual_price 和 xcp_profit 两者的另一个区别在于对待提取管理员手续费 admin_fee 的计量方式上：

• virtual_price 会考虑每次提取管理员手续费时增发的 LP token，即使用通胀的方式计量管理员手续费
• xcp_profit 则不包含增发的 LP token ，而是在提取管理员手续费时，将利润扣除，即不通胀，而是直接减去量化数值

调用 claim_admin_fee() 之后 total_supply 增加，导致 virtual_price 减小（X_cp/total_supply 的分母增大），同时 xcp_profit 会直接扣除利润。

注意代码中费率的计算最后除以2，是因为需要将用于 repegging 部分的利润排除，那部分不属于流动性提供者。

@internal
def _claim_admin_fees():
    # (xcp_profit - xcp_profit_a) is pool's cumulative total profit per LP token
    # self.admin_fee is admin fee rate (now is 50%)
    # @notice: divide 2 is because half of total profit was used 
    # to repeg, they are not belong to Liquidity providors.
    fees: uint256 = (xcp_profit - xcp_profit_a) * self.admin_fee / (2 * 10**10)
    ...
    frac: uint256 = vprice * 10**18 / (vprice - fees) - 10**18
    claimed: uint256 = CurveToken(token).mint_relative(receiver, frac)
    xcp_profit -= fees*2
    self.xcp_profit = xcp_profit
    ...

To Readers

献给读者的一封信:

感谢看到这里仍然还没有放弃的你，非常欣慰在 Defi 研究的道路上我们多了一位同路人，如果有任何关于文章的问题，请毫不犹豫的联系我们。

就像 AC 经常说的那样，Curve Finance 的机制很神奇，要学习可能很难，但请不要放弃。

研究 Curve 的是一个很容易放弃的过程，对于这一点，我想我们最有发言权。

Curve 的研究具有很多的难点：

1. Curve 更加偏数学优化，很多 Defi 代码逻辑是币圈原创。
2. Curve V2 核心合约中 95% 以上的代码由 Curve CEO Michael 一人贡献，注释很少，其他人的给的注释有误
3. 白皮书中有些关键地方 Michael 表述有误，导致理解困难
4. Curve 和 Uniswap 相比缺少他人研究的参考资料

其中最大的难点，我们认为是无法请教别人。大家对Curve的问题都集中在牛顿法和repegging。

About Newton's Method

而要彻底的搞懂 Michael 在牛顿法所运用的技巧和推导的思路，无疑是需要大量的尝试的。众所周知，Curve V2 的方程包含了 N 维，在数学上进行 N 维的推导和证明无疑带来了更大的难度，这也是为什么目前除了Michael没有任何其他第三方团队能够理解这里是如何从数学推导转化为代码的。（请参考我们的文章来感受Michael在此方法中的伟大创新）

Reference and Innovation of Newton's Method Code

About Repegging

一般来说defi的业务代码逻辑参照白皮书去理解是非常直观的。而当我们参照白皮书去看 Curve 的 repeg 过程时，会发现你几乎无法确定 Michael 设计 repeg 的动机和原因，也不能精确理解 repeg 的后果和影响。

造成这种现象的原因有2个，一方面是 repeg 涉及了很多新设计的概念，比如 X_cp 本质要当做 Uniswap 中的流动性 L 来理解。另外一方面是因为repeg过程涉及到的联动的变量和环节太多（请参考我们的流程图）。