Curve v2 CryptoSwap: exchange and fee

Curve v2 CryptoSwap: exchange and fee

Curve v2 CryptoSwap 详解系列：

1. Curve v2 CryptoSwap: white paper
2. Curve v2 CryptoSwap: add and remove liquidity
3. Curve v2 CryptoSwap: exchange and fee
4. Curve v2 CryptoSwap: repegging
5. Curve v2 CryptoSwap: math lib

exchange

交易的逻辑相对于流动性的操作较为简单，与 Uniswap 的 exactInput 接口类似，指定输入的 token 数量，和预期最小的输出数量。

$KD^{N-1}\sum{x_i}+\prod{x_i}=KD^N+(\frac{D}{N})^N$

其不同之处在于两者计算输出数量所使用的平衡公式不同，由于 Uniswap 的公式相对简单，可以直接求解析解，而 Curve 的核心公式更加复杂，无法直接求出解析解，需要借助牛顿法迭代求解。有关牛顿法的详解解析可以参考我们之前的相关文章：

• 英文版 Reference and Innovation of Newton's Method Code
• 中文版 curve V1&V2 牛顿法代码思路及借鉴创新-(对 curve math 库做科普)

exchange 的函数接口如参分别是输入资产 i 数量 dx，输出资产 j，输出数量不能少于 min_dy，返回实际的输出数量。

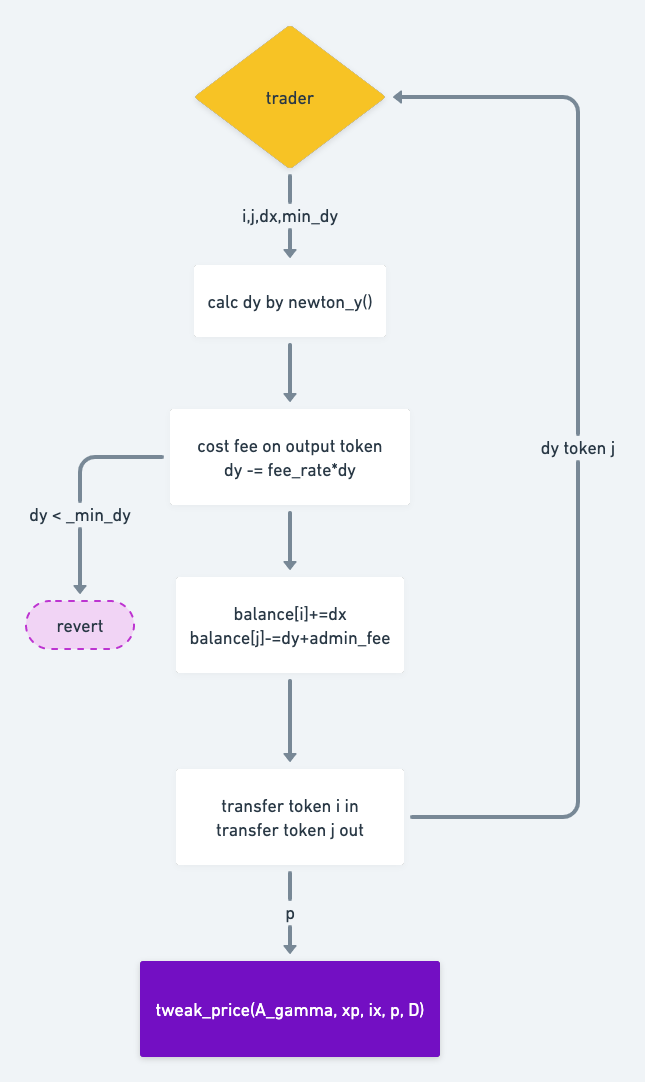
1. 检查入参，资产序号合法，输入资产数量 > 0
2. 转入输入资产
3. 取出 A 和 gamma 系数，如果处于调整期，需要线性计算其值
4. 不考虑手续费的情况下，利用 newton_y 计算出交易后池子内输出资产的 xp，和交易前的 xp 相减，得出输出 dy，更新全局变量 xp, balances
   • 注意 newton_y 计算的结果是价值 (和 xp 同单位)，不是数量 (balance)
   • dy / price_scale[j] 价值 / 价格 得到数量，由于不同 token 的 decimal 可能不同 (不都是 18，例如 USDC 是 6)，所以还要乘以 precisions 变量
5. 转出输出资产
6. 根据 dx dy 计算该笔交易的实际执行价格, 带入 tweak_price 逻辑 (repegging)

@payable
@external
@nonreentrant('lock')
def exchange(i: uint256, j: uint256, dx: uint256, min_dy: uint256, use_eth: bool = False) -> uint256:
    assert not self.is_killed  # dev: the pool is killed
    assert i != j  # dev: coin index out of range
    assert i < N_COINS  # dev: coin index out of range
    assert j < N_COINS  # dev: coin index out of range
    assert dx > 0  # dev: do not exchange 0 coins

    A_gamma: uint256[2] = self._A_gamma()       # cache A and gamma
    xp: uint256[N_COINS] = self.balances        # xp container, cache balances, will multiply price later
    ix: uint256 = j                             # the index of output coin
    p: uint256 = 0                              # init price of exchanging
    dy: uint256 = 0                             # init amount_out

    if True:  # scope, simular with {} in solidity
        _coins: address[N_COINS] = coins
        if i == 2 and use_eth:      # Using eth,  msg.value as amount in, then trans ETH to WETH
            assert msg.value == dx  # dev: incorrect eth amount
            WETH(coins[2]).deposit(value=msg.value)
        else:                       # msg.value must be zero when exchaging without eth
            assert msg.value == 0  # dev: nonzero eth amount
            # assert might be needed for some tokens - removed one to save bytespace
            ERC20(_coins[i]).transferFrom(msg.sender, self, dx)

        y: uint256 = xp[j]          # cache token_out's reserve
        x0: uint256 = xp[i]         # cache token_in's reserve
        xp[i] = x0 + dx             # dx is amount_in, xp is still balances, not balance*price
        self.balances[i] = xp[i]

        # cache price_scale multiply balance get xp
        price_scale: uint256[N_COINS-1] = empty(uint256[N_COINS-1])
        packed_prices: uint256 = self.price_scale_packed
        for k in range(N_COINS-1):
            price_scale[k] = bitwise_and(packed_prices, PRICE_MASK)  # * PRICE_PRECISION_MUL
            packed_prices = shift(packed_prices, -PRICE_SIZE)

        precisions: uint256[N_COINS] = PRECISIONS
        xp[0] *= PRECISIONS[0]
        for k in range(1, N_COINS):
            xp[k] = xp[k] * price_scale[k-1] * precisions[k] / PRECISION

        prec_i: uint256 = precisions[i]

        # Recalculate A and gamm when they are ramping
        if True:
            t: uint256 = self.future_A_gamma_time
            if t > 0:
                x0 *= prec_i
                if i > 0:
                    x0 = x0 * price_scale[i-1] / PRECISION
                x1: uint256 = xp[i]  # Back up old value in xp
                xp[i] = x0
                self.D = Math(math).newton_D(A_gamma[0], A_gamma[1], xp)
                xp[i] = x1  # And restore
                if block.timestamp >= t:
                    self.future_A_gamma_time = 1

        prec_j: uint256 = precisions[j]     # cache the presision of token_out

        # newton_y is the newton's method to calculate xp_out (value, not amount)
        # dy is the difference between after and before of xp_out
        dy = xp[j] - Math(math).newton_y(A_gamma[0], A_gamma[1], xp, self.D, j)
        xp[j] -= dy
        # To prevent the loss of precision of the subsequent division operation (LP interests are preferred)
        dy -= 1

        # Convert value to amount (dy/price), when token_out is not coin[0]
        if j > 0:
            dy = dy * PRECISION / price_scale[j-1]
        dy /= prec_j

        dy -= self._fee(xp) * dy / 10**10       # cost fees on token_out
        assert dy >= min_dy, "Slippage"         # If amount_out < min_amount_out after cost fees, revert
        y -= dy

        self.balances[j] = y                    # update balances of reserves
        # Transfer token_out to user
        if j == 2 and use_eth:
            WETH(coins[2]).withdraw(dy)
            raw_call(msg.sender, b"", value=dy)
        else:
            ERC20(_coins[j]).transfer(msg.sender, dy)

        # update xp
        y *= prec_j
        if j > 0:       # If not coin[0], multiply price get value
            y = y * price_scale[j-1] / PRECISION
        xp[j] = y

        # calculate price, pass it to tweak_price as last_price input
        # There three kind of case:
        # 1. token_in and token_out both are not coins[0], p = amount_in * price / amount_out
        # 2. 3. one of token_in and token_out is coins[0], using coin[0] as the dividend
        # Notice: dx and dy both are amount, not value
        if dx > 10**5 and dy > 10**5:
            _dx: uint256 = dx * prec_i
            _dy: uint256 = dy * prec_j
            if i != 0 and j != 0:
                p = bitwise_and(
                    shift(self.last_prices_packed, -PRICE_SIZE * convert(i-1, int256)),
                    PRICE_MASK
                ) * _dx / _dy  # * PRICE_PRECISION_MUL
            elif i == 0:
                p = _dx * 10**18 / _dy
            else:  # j == 0
                p = _dy * 10**18 / _dx
                ix = i

    self.tweak_price(A_gamma, xp, ix, p, 0)

    log TokenExchange(msg.sender, i, dx, j, dy)

    return dy

fees

根据 xp 动态计算当前手续费水平，规则参照 Dynamic fees 的公式。

$f=g \cdot f_{mid}+(1-g)\cdot f_{out}$

@internal
@view
def _fee(xp: uint256[N_COINS]) -> uint256:
    # f is the g in the formula
    f: uint256 = Math(math).reduction_coefficient(xp, self.fee_gamma)
    return (self.mid_fee * f + self.out_fee * (10**18 - f)) / 10**18


@external
@view
def fee() -> uint256:
    return self._fee(self.xp())


@external
@view
def fee_calc(xp: uint256[N_COINS]) -> uint256:
    return self._fee(xp)

reduction_coefficient() 是 CurveCryptoMath 合约中用于计算 g 的函数，参见 CurveCryptoMath#reduction_coefficient()

Fees of add liquidity imbalanced

上一章中提到如果用户不平衡的操作流动性，Curve 会对其部分流动性收取手续费，接下来我们将详细探究其运作逻辑。

Sdiff/S

假设现在用户 A 向 tricrypto 池中添加一笔不平衡的流动性，该添加操作 USDT-WBTC-WETH 增加的 xp 分别有 [100, 200, 300] （计算时都会将 balance 乘以 price ，为了简化问题，我们直接假设 xp 的增加数值）。这笔不平衡的添加，会让 USDT 和 WETH 的价值相差更大，所以我们需要累加这些引发偏离平衡的量来计算手续费。在 v2 CryptoSwap 中具体的逻辑如下：

1. 计算该笔添加的总价值 S = sum(xp)
2. 计算该笔添加的平均价值 avg = S / N
3. 累加每种资产添加价值与 avg 偏差量 Sdiff = sum(|xp - avg|)，注意是累加差的绝对值
4. 将 Sdiff 和 S 的比值作为手续费的调整系数，直接在操作用户的 LP token 中扣除

所以 添加/移除 的越不平衡，手续费将收取的越多，反过来，如果添加的每种资产价值相等，则不会收取手续费。

那么添加 [100, 200, 300] 的情况如下：

S = 100 + 200 + 300 = 600
avg = 600 / 3 = 200
Sdiff = |100 - 200| + |200 - 200| + |300 - 200| = 200

最后我们得到了手续费的调整系数 Sdiff/S = 200/600。

N/(4*(N-1))

除了 Sdiff / S 这个与不平衡程度相关的调整系数，流动性操作计算手续费还有一个和 N 相关的调整系数 N / (4 * (N - 1))。

因为 N 越小，每种资产的价格受到不平衡的影响越大，N 越大每种资产价格受到不平衡的影响反而越小。该调整系数的值处于区间 [1/2, 1/4) 。

• 当 N = 2 时，系数最大，为 2 / (4 * (2 - 1)) = 1/2
• 当 N 趋近于无穷大时，系数最小，$\lim_{N \to +\infty} \frac{N}{4 * (N - 1)} = \frac{1}{4}$

calculate token fee

在 v2 CryptoSwap 中，_calc_token_fee() 函数是根据流动性变化量的不平衡程度和 N 相关的系数计算手续费率的函数，入参 amounts 是流动性变化的量（增加或减少）。例如添加流动性，则考虑的是本次操作每种资产分别增加了多少 xp，注意这里是 xp，不是数量。

函数将返回调整后的手续费率，用于直接在 LP token 上扣除手续费。

fee_rate = fee_rate_base * (Sdiff / S) * N / (4 * (N - 1))

接下来我们看看如何具体的实现这一计算过程:

• 首先计算 xp 的改变量，计算增加或减少的绝对值，存入 amountsp 数组
• 将 amountsp 传入 _calc_token_fee() 函数
  • 根据池子现有 xp 利用 fee(xp) 函数计算交易的基准费率，注意此时 xp 已经根据 amountsp 调整过
  • 费率乘以系数 N / (4 * (N - 1))
  • 计算 amountsp 的总和 S
  • 计算 amountsp 的累加偏差量 Sdiff
  • 最后费率再乘以系数 Sdiff / S
• 至此我们得到了一个考虑了 N 的数值和流动性操作的不平衡程度的调整后的费率
• 最后直接在 LP token 的数量扣除，将价值留在池子内部，就完成了不平衡流动性的手续费收取

# amountsp is an array of delta xp of every coin,
# it is _calc_token_fee() input params `amounts`.
# notice: amountsp here is xp, the product of price and balance
for i in range(N_COINS):
    if amounts[i] > 0:
        amountsp[i] = xp[i] - xp_old[i]
        ...

# according to the degree of imbalance and the coefficient of N calculate fee_rate
# notice: amounts is amountsp
@view
@internal
def _calc_token_fee(amounts: uint256[N_COINS], xp: uint256[N_COINS]) -> uint256:
    # fee = sum(amounts_i - avg(amounts)) * fee' / sum(amounts)
    fee: uint256 = self._fee(xp) * N_COINS / (4 * (N_COINS-1))
    S: uint256 = 0
    for _x in amounts:
        S += _x
    avg: uint256 = S / N_COINS
    Sdiff: uint256 = 0
    for _x in amounts:
        if _x > avg:
            Sdiff += _x - avg
        else:
            Sdiff += avg - _x
    return fee * Sdiff / S + NOISE_FEE

# we cost fee directly on d_token which is
# the number of LP token that user will get
d_token_fee = self._calc_token_fee(amountsp, xp) * d_token / 10**10 + 1
...

calc_token_fee

计算不平衡的添加流动性时，过程中产生的交易手续费。amounts 是 xp 的增量， xp 是当前 xp，返回添加流动性过程中产生的手续费。

注意： 返回手续费的单位是以 LP token 为计量的，该数量将直接在 mint 出来的 LP token 数量上相减，参见 add_liquidity 的代码

1. 计算增加价值 S 和平均数 avg
2. 每个资产增量和 avg 的差量取绝对值累加作为 Sdiff
3. fee = sum(amounts_i - avg(amounts)) / sum(amounts) * fee'
   • 按照不平衡部分和总增量的比例来收取
   • 观察整个过程的运算单位，最后是 Sdiff (价值) / S (价值)，两个价值单位被抵消，固最后的得数是一个比例（无单位），因为该函数将被用于计算 LP token 手续费扣减数量
   • NOISE_FEE 是噪音参数，极小的值，但使得返回值不能为零，防止可能的攻击

@view
@internal
def _calc_token_fee(amounts: uint256[N_COINS], xp: uint256[N_COINS]) -> uint256:
    # fee = sum(amounts_i - avg(amounts)) * fee' / sum(amounts)
    fee: uint256 = self._fee(xp) * N_COINS / (4 * (N_COINS-1))
    S: uint256 = 0
    for _x in amounts:
        S += _x
    avg: uint256 = S / N_COINS
    Sdiff: uint256 = 0
    for _x in amounts:
        if _x > avg:
            Sdiff += _x - avg
        else:
            Sdiff += avg - _x
    return fee * Sdiff / S + NOISE_FEE


@external
@view
def calc_token_fee(amounts: uint256[N_COINS], xp: uint256[N_COINS]) -> uint256:
    return self._calc_token_fee(amounts, xp)

Fees of remove liquidity imbalanced

calc_withdraw_one_coin

计算移除流动性只收取单一资产，可以收到的具体资产数量

• 在 D 值上扣除手续费，而不是输出资产 y，即，直接减少用户可赎回的 LP token 作为手续费
• dD 是根据移除 LP token 和 totalSupply 比例计算的 delta D
• 先在 dD 上扣除手续费，其逻辑是直接向 dD 的一半收取手续费，因为此时是赎回单一资产，相当于其中一半需要用其他资产交易成该资产，所以直接 / 2
• 根据新的 D 值使用牛顿法计算出该资产的数量 y

curve v2 不平衡的移除流动性只有获取单一资产的接口，对于手续费的调整系数直接简化为 1/2，而非 N/(4*(N-1))

@internal
@view
def _calc_withdraw_one_coin(A_gamma: uint256[2], token_amount: uint256, i: uint256, update_D: bool,
                            calc_price: bool) -> (uint256, uint256, uint256, uint256[N_COINS]):
    token_supply: uint256 = CurveToken(token).totalSupply()
    assert token_amount <= token_supply  # dev: token amount more than supply
    assert i < N_COINS  # dev: coin out of range

    xx: uint256[N_COINS] = self.balances    # cache balances
    xp: uint256[N_COINS] = PRECISIONS       # xp container, cache precision and mutiply price later
    D0: uint256 = 0                         # cache D value

    # calculate xp = balances * price
    price_scale_i: uint256 = PRECISION * PRECISIONS[0]
    if True:  # To remove packed_prices from memory
        packed_prices: uint256 = self.price_scale_packed
        xp[0] *= xx[0]
        for k in range(1, N_COINS):
            p: uint256 = bitwise_and(packed_prices, PRICE_MASK)  # * PRICE_PRECISION_MUL
            if i == k:
                price_scale_i = p * xp[i]
            xp[k] = xp[k] * xx[k] * p / PRECISION
            packed_prices = shift(packed_prices, -PRICE_SIZE)

    # Use newton's method to update D
    if update_D:
        D0 = Math(math).newton_D(A_gamma[0], A_gamma[1], xp)
    else:
        D0 = self.D

    D: uint256 = D0

    # Charge the fee on D, not on y, e.g. reducing invariant LESS than charging the user
    fee: uint256 = self._fee(xp)
    dD: uint256 = token_amount * D / token_supply
    D -= (dD - (fee * dD / (2 * 10**10) + 1))
    y: uint256 = Math(math).newton_y(A_gamma[0], A_gamma[1], xp, D, i)
    dy: uint256 = (xp[i] - y) * PRECISION / price_scale_i
    xp[i] = y

    # Calculate price of this trade，pass it to tweak_price.
    # The logic is simular with add liquidity
    p: uint256 = 0
    if calc_price and dy > 10**5 and token_amount > 10**5:
        # p_i = dD / D0 * sum'(p_k * x_k) / (dy - dD / D0 * y0)
        S: uint256 = 0
        precisions: uint256[N_COINS] = PRECISIONS
        last_prices: uint256[N_COINS-1] = empty(uint256[N_COINS-1])
        packed_prices: uint256 = self.last_prices_packed
        for k in range(N_COINS-1):
            last_prices[k] = bitwise_and(packed_prices, PRICE_MASK)  # * PRICE_PRECISION_MUL
            packed_prices = shift(packed_prices, -PRICE_SIZE)
        for k in range(N_COINS):
            if k != i:
                if k == 0:
                    S += xx[0] * PRECISIONS[0]
                else:
                    S += xx[k] * last_prices[k-1] * precisions[k] / PRECISION
        S = S * dD / D0
        p = S * PRECISION / (dy * precisions[i] - dD * xx[i] * precisions[i] / D0)

    return dy, p, D, xp


@view
@external
def calc_withdraw_one_coin(token_amount: uint256, i: uint256) -> uint256:
    return self._calc_withdraw_one_coin(self._A_gamma(), token_amount, i, True, False)[0]

Compare with v1 StableSwap in imbalanced liquidity

在 v1 StableSwap 中，对于不平衡的流动性计算手续费和 v2 CryptoSwap 有所不同。

• 计算流动性改变后的 balances，然后用 new_balances 代入牛顿法中计算出新的 D 值 D1
• 根据 D1/D0 即 D 的变化比例，同比放大每种资产的 balance，得出 ideal_balance

同样以添加流动性为例，v1 StableSwap 涉及到不平衡流动性手续费的代码如下：

# 3pool.vy
@external
@nonreentrant('lock')
def add_liquidity(amounts: uint256[N_COINS], min_mint_amount: uint256):
    ...

    # fee_rate multiple coefficient on N
    _fee: uint256 = self.fee * N_COINS / (4 * (N_COINS - 1))

    # add amounts on balances get new_balances
    for i in range(N_COINS):
        in_amount: uint256 = amounts[i]
        new_balances[i] = old_balances[i] + in_amount
        ...

    # calculate new D by new_balances as D1
    # D0 is D old value
    D1: uint256 = self.get_D_mem(new_balances, amp)
    assert D1 > D0

    # Only account for fees if we are not the first to deposit
    for i in range(N_COINS):
        ideal_balance: uint256 = D1 * old_balances[i] / D0
        difference: uint256 = 0
        if ideal_balance > new_balances[i]:
            difference = ideal_balance - new_balances[i]
        else:
            difference = new_balances[i] - ideal_balance
        fees[i] = _fee * difference / FEE_DENOMINATOR

    ...