Curve v2 CryptoSwap: add and remove liquidity

Curve v2 CryptoSwap 详解系列：

1. Curve v2 CryptoSwap: white paper
2. Curve v2 CryptoSwap: add and remove liquidity
3. Curve v2 CryptoSwap: exchange and fee
4. Curve v2 CryptoSwap: repegging
5. Curve v2 CryptoSwap: math lib

Curve 在 v1 StableSwap 中实现了稳定资产之间的 AMM， v2 CryptoSwap 将比其更进一步，不仅仅支持稳定资产之间的交易，而是拓展到通用的 AMM，可以是相互之间不锚定的资产。为了实现这个目标，v2 CryptoSwap 将比 v1 StableSwap 复杂许多。

CryptoSwap-relationship:

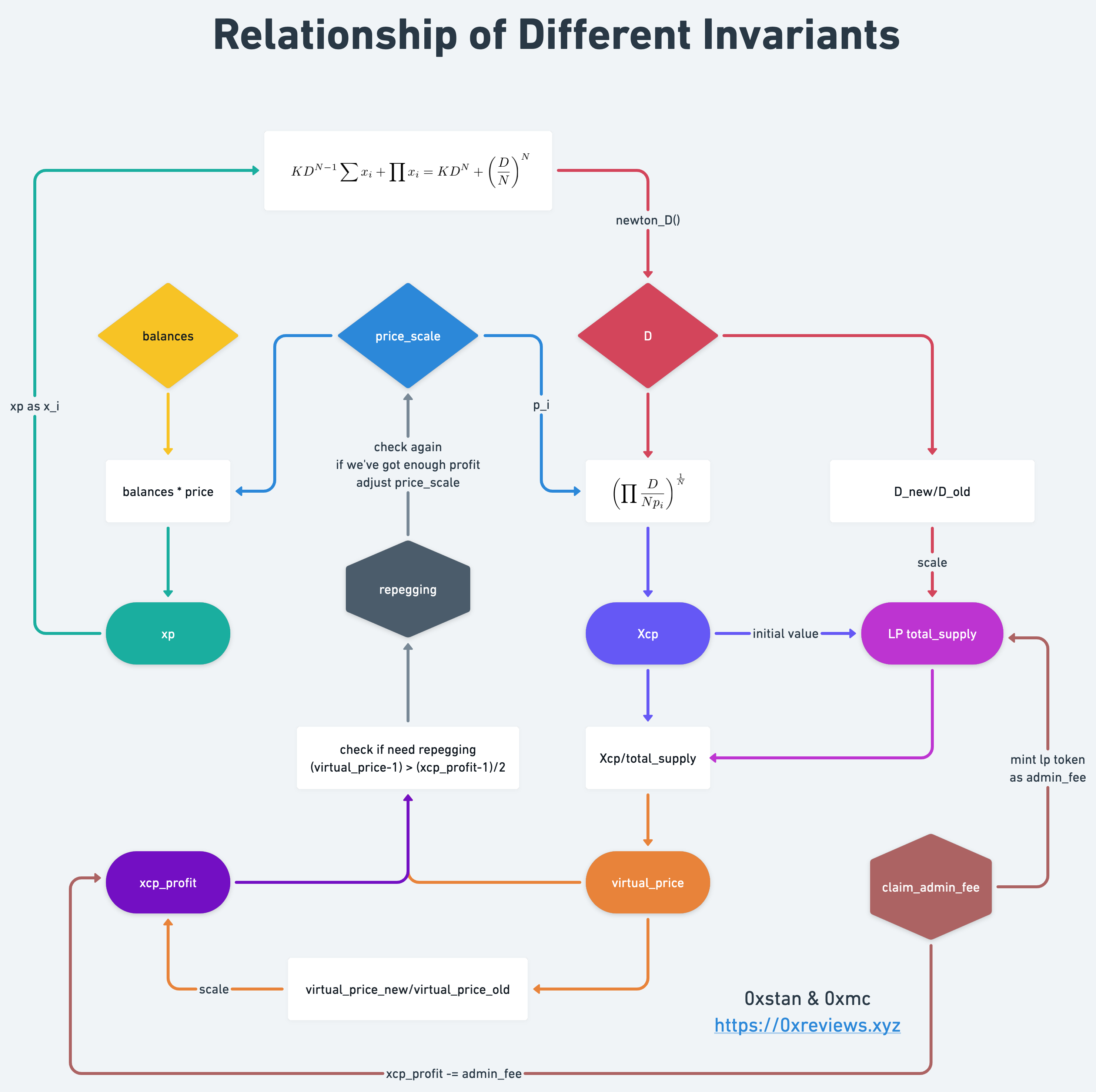
上图是 CryptoSwap 中各个概念的关系图，我们简化了许多细节，尽量只保留主要的逻辑。尽管如此，想要理解其工作原理仍然不是一件容易的事情，接下来我们将深入到 CryptoSwap 的代码中，探寻其业务逻辑和运行细节。

我们将假定你已经了解 v1 StableSwap 的运行原理，如果你还没有，可以先阅读我们对 StableSwap 的解析：Curve v1 StableSwap code review

special StableSwap--ypool

StableSwap 顾名思义，池中的资产之间可以认为是锚定的同一标的资产，例如 DAI-USDC-USDT (3pool) 池内三种资产都是锚定美元的 token，ETH-stETH 池内资产都是锚定 ETH 。池内资产之间的价格，其实可以认为一直都是 1。之所以在交易时会有价格滑点，除了扣除手续费带来的影响，还有 v1 核心平衡等式造成的价格滑点，保证池子的健康运行，不会被外部套利者拿走池内过多的价值。

这个逻辑可能会有些反直觉，例如 uniswap 的交易池子中，其内部价格将随着资产的比例不同而变化，但是在 3pool 中其内部价格是写死的 1，交易时的滑点，实际上主要是由牛顿法求解得出。

当我们需要从 StableSwap 拓展到 CryptoSwap 时，资产将不再仅限于锚定同一资产标的的 token，如果内部价格还是恒定的 1，显然是不可行的。这时就需要动态调整的内部价格，实际上 v1 StableSwap 有一种特殊的池子已经做出了这种实现，那就是 ypool。

由于 ypool 中的资产是一种内增值的资产，例如 yDAI 是 yearn.finance 的封装资产，1 yDAI 所能兑换的底层资产(underlying coin) DAI 数量实际上是随着利息增长的。所以如果 StableSwap 的内部价格恒定为 1，当 yDAI 的兑换率增长时，每个 1 yDAI 能兑换更多的 DAI，这将造成大量的套利交易涌入，拿走便宜的 yDAI，兑换成更多的 DAI。

为了解决这个问题，ypool 不再将 RATES 作为常量(1:1)，而是使用一个函数 stored_rates()，实时的查询 yToken 和底层资产的兑换率。如此，计算 xp 时, xp = rates * balance，xp 将受到实时变化的 rates 的影响。

实际上这里实时变化的 rates 即为 CryptoSwap 的内部缩放价格。

# /contract/y/StableSwapY.vy
@private
@constant
def _stored_rates() -> uint256[N_COINS]:
    result: uint256[N_COINS] = PRECISION_MUL
    for i in range(N_COINS):
        result[i] *= yERC20(self.coins[i]).getPricePerFullShare()
    return result


@private
@constant
def _xp(rates: uint256[N_COINS]) -> uint256[N_COINS]:
    result: uint256[N_COINS] = rates
    for i in range(N_COINS):
        result[i] = result[i] * self.balances[i] / PRECISION
    return result

We already do that with compound and y pools on curve.fi. -- 《Automatic market-making with dynamic peg》

Three kinds of price

在 v2 CryptoSwap 中，记录了三种价格

• price_scale_packed 存放内部缩放价格，也是核心公式中的 p，计算 D, xp, X_cp 都将使用该价格计算
• price_oracle_packed 内部 EMA 预言机价格，用于调整内部缩放价格 (price_scale)
• last_prices_packed 最后一次交易产生的价格，用于更新内部预言机价格 (price_oracle)

上述三种价格的更新是在 repegging 逻辑中进行的：

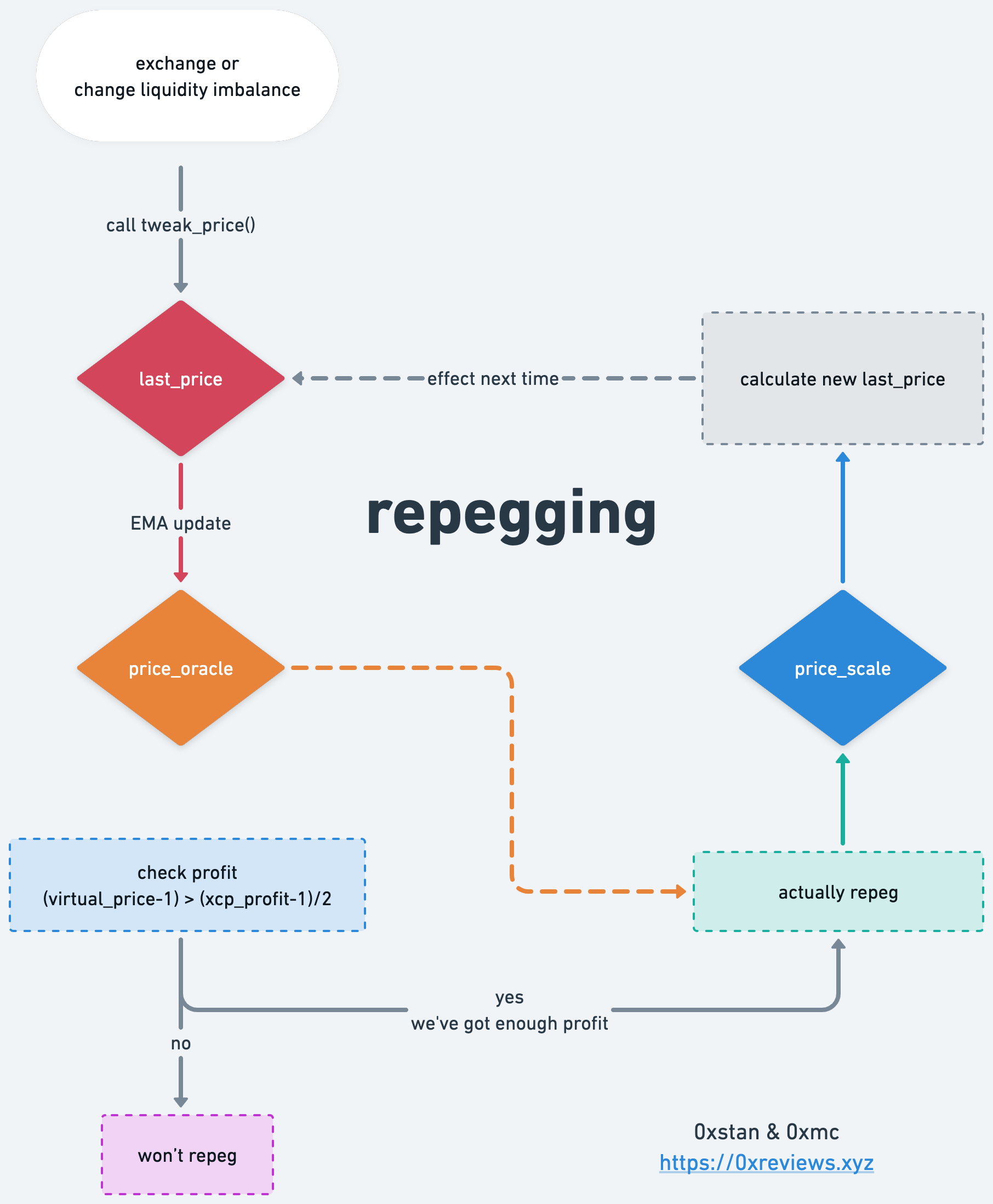
这三种价格的关系可以视为循环关系，其核心目的是为了在不依赖于外部的价格预言机的情况下，恰当的调整内部缩放价格。

首先是在交易时产生了实际交易价格 last_price，这是由交易的输入和输出的比值产生的，即 last_price = dy/dx。

接着 last_price 将遵照时间加权的规则更新内部预言机价格 price_oracle。

最后会用 price_oracle 更新 price_scale，当然，只有当池子积累了足够的利润的时候，才会发生调整，详细逻辑我们将在 Repegging of Curve v2 CryptoSwap 部分探究。

由于交易时的 dy ，是通过牛顿法计算，而牛顿法的计算公式是由核心平衡等式推导而来，其中的 p 即为 price_scale，所以如果 price_scale 发生了调整，将会影响到下一次的交易。

Prices data structure

如果阅读 v2 CryptoSwap 的源码，会注意到价格变量名字有个 packed 后缀，并且是 uint256 值类型，而不是数组类型。因为 storage 存储 gas 开销非常高昂，这里 Curve 对价格存储数据结构做了优化。即不用数组，而是将价格合并到同一个 uint256 类型。

这里的价格，指的是每种资产对第一种资产的价格，即 coins[1]-coins[0] 和 coins[2]-coins[0]，而 coins[0]-coins[0] 不需要存储，因为和自身的比值将永远是 1。

首先我们省略了 coins[0] 的价格，然后将 coins[1] 价格存储到第 128 到 255 位， coins[2] 存储到第 0 到 127 位。

注意左边是 coins[2],右边是 coins[1]。

# Exclude coins[0] because it is always equels 1.
# | bit 0 - 127 ｜ bit 128 - 255 |
# |   coins[2]   |    coins[1]     |
price_scale_packed: uint256

我们来看看 prices packed 的存储过程，以 tricrypto 为例（N = 3）：

• 我们要把 p_new 价格数组(包含 2 个价格元素)打包到 packed 变量中
• 初始化一个价格缓存容器 packed_prices
  • 因为直接在 storage 上操作会承担高昂的 gas，利用缓存容器将价格计算好，最后只需要一次 SSTORE 操作即可
  • 令其等于 0 ，我们得到了一个 256 位全是 0 的容器
• 将价格分别存储到容器的不同的区域(左侧 bit 0-127, 右侧 bit 128-255)
  • 利用 for 循环操作，因为排除了 coins[0], 我们实际上只需要存储价格 N-1 次 (2 次)
  • k = 0 时
    • packed_prices 左移 PRICE_SIZE 位，实际上仍然是 0
    • p_new[N_COINS-2 - k] 是 p_new[1] 存储到容器的右侧区域
  • k = 1 时
    • packed_prices 左移 PRICE_SIZE 位，将上一次存储到右侧区域的价格，移动到左侧区域，右侧区域补 0
    • p_new[N_COINS-2 - k] 是 p_new[0] 存储到容器的右侧区域
  • 至此我们将容器组合成了计算好的 packed 结构
• 将计算好的容器的值赋值给 storage 中存储的全局 prices 变量

# /tricrypto.vy
# init a packed data container, because it's a uint256
# so we get 256 bits, every bit is 0
packed_prices = 0
# loop N - 1 times, because we exclude coins[0]
for k in range(N_COINS-1):
    # left shift container
    # and put p_new to right part of it (bit 128-255)
    packed_prices = shift(packed_prices, PRICE_SIZE)
    p: uint256 = p_new[N_COINS-2 - k]
    assert p < PRICE_MASK
    packed_prices = bitwise_or(p, packed_prices)
# save value to storage variable at last
# only doing SSTORE onece, will save gas
self.price_scale_packed = packed_prices

_packed_view(k: uint256, p: uint256) 是从 packed 结构中提取价格的方法

• 断言 k < N_COINS-1，因为价格不包含 coin[0]，所以索引 k 需要减 1
• p 是需要解构的价格 packed 结构数据
• bitwise_and() 是 vyper 语言中的内建位运算函数，按位与
• shift(x: uint256, _shift: int128) 是 vyper 语言的内建位移函数， _shift 大于 0 代表左移，小于 0 代表右移
• PRICE_MASK 是 price 的最大值，即二进制全是 1 的掩码

# EVM's largest unsigned intege type is uin256,
# so 256 bits is the largest place to save prices data.
# According to N, we decide how many bits every price data is.
# divide 256 by N-1, because we Exclude coins[0]
PRICE_SIZE: constant(int128) = 256 / (N_COINS-1)

# The mask that its all bits are 1
# e.g. 2**3 is binary 1000, (2**3 - 1) is binary 111
# PRICE_MASK here is binary 1111....111 (there are PRICE_SIZE 1)
PRICE_MASK: constant(uint256) = 2**PRICE_SIZE - 1

@internal
@view
def _packed_view(k: uint256, p: uint256) -> uint256:
    assert k < N_COINS-1
    # According to index k to right shift value
    # then extra price data with mask
    return bitwise_and(
        shift(p, -PRICE_SIZE * convert(k, int256)),
        PRICE_MASK
    )

还是以 tricrypto 池子举例，假设我们现在需要提取 WETH 的价格，那么：

• N = 3 因为池子有三种资产， k = 1 因为 packed 结构数据中，不包含 USDT (coin[0]), 所以是从 WBTC 开始存储，k 是 0 就代表了 WBTC，k 是 1 就代表了 WETH
• PRICE_SIZE = 256 / 2 = 128
• PRICE_MASK = 2**128 - 1 是具有 128 位的全是 1 的掩码
• 将 packed 数据右移 k * 128 位
  • 如果 k = 0 实际上不会位移
  • 这里 k = 1 就是右移 1 * 128 位

三种价格的提取将复用 _packed_view() 函数

@external
@view
def price_oracle(k: uint256) -> uint256:
    return self._packed_view(k, self.price_oracle_packed)


@external
@view
def price_scale(k: uint256) -> uint256:
    return self._packed_view(k, self.price_scale_packed)


@external
@view
def last_prices(k: uint256) -> uint256:
    return self._packed_view(k, self.last_prices_packed)

xp and its decimal

在白皮书公式中出现的 x_i 都是 xp，余额与价格的乘积， 即 价值。实际上 v1 StableSwap 中的 x_i 也是 xp，只不过因为其价格大部分为 1，很容易混淆成余额 balance。

xp = balance * price_scale

由于不同 token 的精度 decimal 不同，计算时需要统一为 1e18，PRECISIONS 为统一精度的数组：

# tricrypto

PRECISION: constant(uint256) = 10 ** 18  # The precision to convert to

PRECISIONS: constant(uint256[N_COINS]) = [
    1000000000000,  # USDT's decimal is 6, should times 1e12
    10000000000,    # WBTC's decimal is 8, should times 1e10
    1,              # WETH's decimal is 18, should times 1
]

例如在 tricrypto 中，池内三种资产为 USDT-WBTC-WETH, 其精度分别为 6, 8, 18，所以该数组中正好存放了可以将 balance 精度统一为 1e18 的乘数，然后再与价格相乘。由于价格 price_scale 也是 1e18 的精度，所以乘积的精度将为 1e36。

然而我们只需要保留 1e18 的数值精度就足够精确，所以最后还要除以 PRECISION (1e18) 来为后续计算预留更多的空间（避免数值溢出）, 最终 xp 的精度也将是 1e18。

@internal
@view
def xp() -> uint256[N_COINS]:
    result: uint256[N_COINS] = self.balances
    packed_prices: uint256 = self.price_scale_packed

    precisions: uint256[N_COINS] = PRECISIONS

    result[0] *= PRECISIONS[0]
    for i in range(1, N_COINS):
        p: uint256 = bitwise_and(packed_prices, PRICE_MASK) * precisions[i]  # * PRICE_PRECISION_MUL
        result[i] = result[i] * p / PRECISION
        packed_prices = shift(packed_prices, -PRICE_SIZE)

    return result

Quantification of liquidity

添加流动性的主要问题在于如何衡量用户添加的流动性。在 CryptoSwap 中思路和 v1 StableSwap 一致，也是用 D 的变化来同比变化 LP token 的总量，增发的部分即为用户当前获取的 LP token 数量。

需要注意的是，我们不能将 D 等价于流动性。

这一点和 Uniswap 不同，不论是 UniswapV2 的 K 还是 UniswapV3 的 L， 都能很直观的与流动性挂钩，或者说他们就是 Uniswap 定义下的流动性。但是在 Curve 的平衡方程中，$(\frac{D}{N})^N$ 只有在价格处于平衡点时，才能与流动性等价。

UniswapV2 的 K 实际上就是 $(\frac{D}{N})^N$，而 UniswapV3 的 L 就是括号内的 D/N，因为当价格处于平衡点时，池内的 x_i 都相等，也就是 D/N

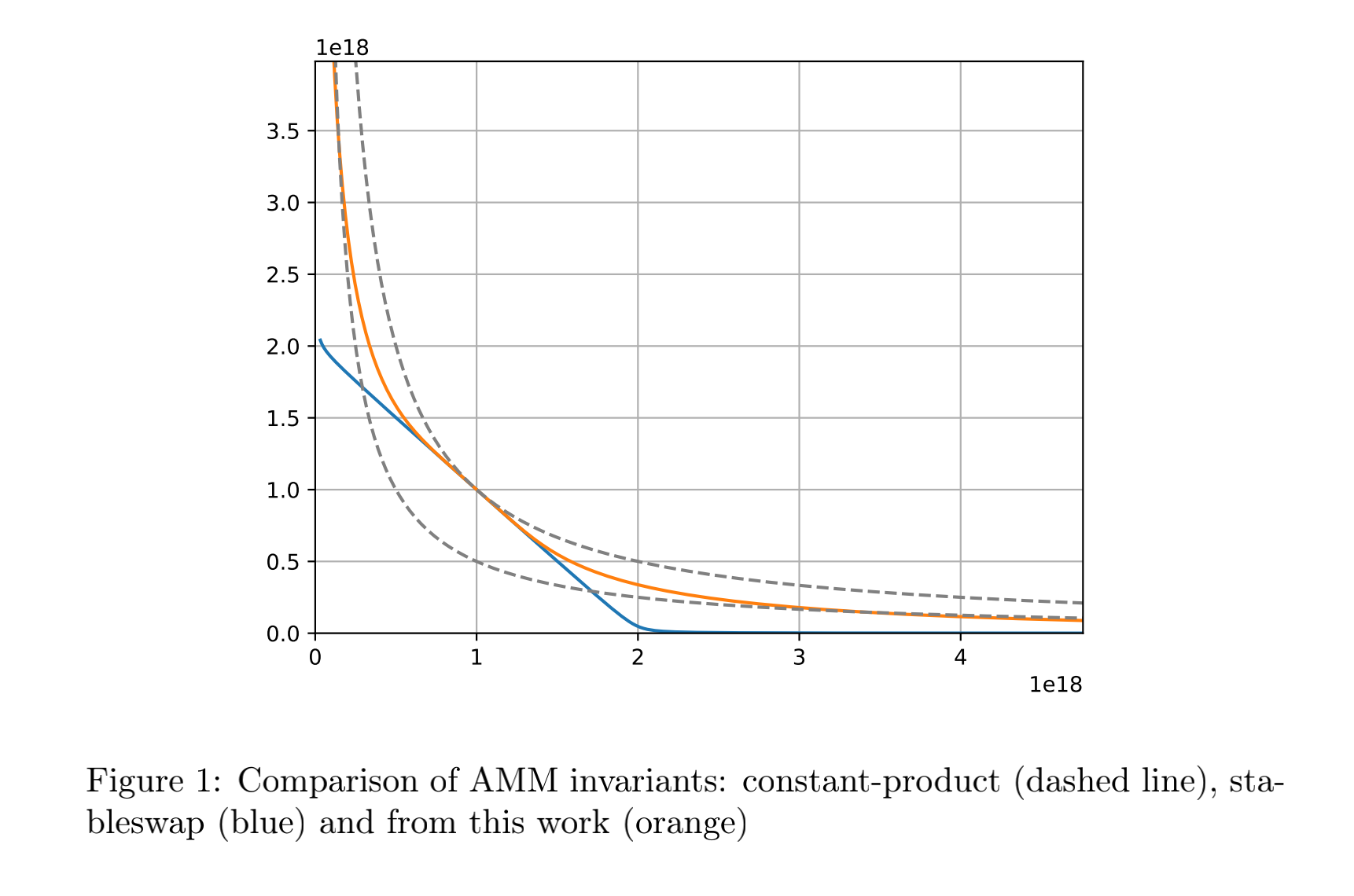
上图中橙色线与蓝色线还有灰色虚线相交的点，即为价格平衡点。

橙色线：$KD^{N-1}\sum{x_i}+\prod{x_i}=KD^N+(\frac{D}{N})^N$

虚线：$\prod{x_i}=(\frac{D}{N})^N$

很容易看出当 $D=\sum{x_i}$ 时，同时满足上述两个方程，是两个曲线的唯一的交点，D 是在价格处于平衡点时各个资产 xp 之和。换言之，离开了平衡点，便不再满足这个关系。

D 不能直接代表流动性，但是却与流动性正相关，在 curve 中对于流动性的增减，都是以 D 的变化来对 LP token 的发行总量进行同比变化，即

d_token = D_new / D_old * total_supply # d_token is delta token

所以只需要根据变化后的 xp 值代入核心平衡方程，使用牛顿法求解新的 D 值，就能得出 LP token 的变化量。关于牛顿法的解析，参见 Curve newton's method。

如果用户严格按照池子当前资产比例添加，那么按照上述逻辑增减流动性是没问题的。但是如果用户没有按照比例添加或移除呢？

交易会引发价格改变，或者准确的说，交易会引起滑点的变化（CryptoSwap 的内部价格可能在交易后没有变化）。例如用户 A 用 100 USDT 交换出 WETH，紧接着用户 B 也用 100 USDT 交换 WETH，理论上 B 换出的 WETH 应该比 A 少，B 承受的滑点更大。原因在于池中的 USDT 和 WETH 的比例发生了变化，其 xp 值改变，导致计算出的交易输出量变化。

那么，如果用户在添加或移除流动性时，资产价值改变的量不平衡，那么池内的资产比例也会发生变化，也将影响交易的滑点，甚至的内部的缩放价格。增减流动性的操作，实际上是可以组合成一笔完整的交易。例如用户在第一次操作添加流动性，只添加 USDT ，然后第二次操作流动性，只移除 WETH，两次操作组合起来，实际就是一笔完整的交易操作。

所以对于流动性的操作，我们需要针对不平衡部分的流动性操作收取交易费用，其计算细节将在下一章展开，此处暂且按下不表。

add_liquidity

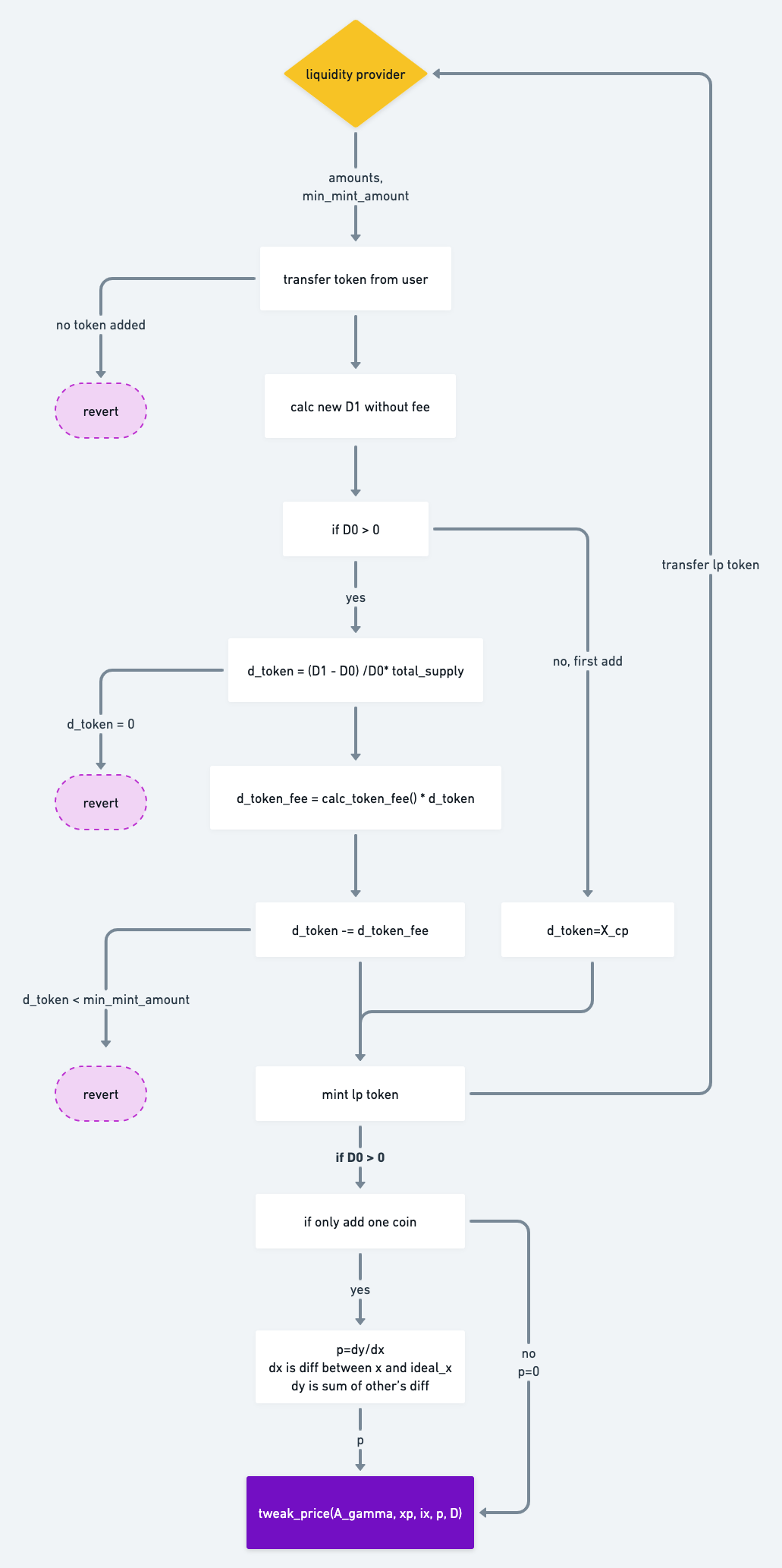
添加流动性，每种资产各添加多少 token 数量 amounts，最少要求获得多少 lp token min_mint_amount。

1. 将新增 amounts 加入资产余额，计算新的 xp，然后牛顿法求新的 D 值
2. 若池子首次添加流动性
   • 此时 d_token = token_supply = xcp，即令 virtual price = 1
   • 更新池子的全局变量，D, virtual_price, xcp_profit, mint lp token
   • 流程结束，不需要对价格做调整
3. 若池子已有流动性
   • 根据新旧 D 值的比例，同比放大 token_supply 计算差值
   • 扣除手续费，为用户 mint 扣除之后的 lp token 数量
     • _calc_token_fee(amountsp, xp) 计算出每单位 lp token 需要收取的费用，再乘以 d_token 就是总共要收取的手续费
   • 若此次只有单一资产添加流动性，将根据公式计算出该资产的价格变化
   • p_i * (dx_i - dtoken / token_supply * xx_i) = sum{k!=i}(p_k * (dtoken / token_supply * xx_k - dx_k))
     • dtoken / token_supply * xx_i 表示用新的 D 值同比计算出来的，不改变价格情况下的，资产 i 的理论数量（因为实际情况只添加了资产 i，池子价格必然发生了变化）
     • 代码中 S = sum{k!=i}(p_k * (dtoken / token_supply * xx_k))
       • 因为只添加了资产 i，所以 dx_k 为 0 可以省略
       • 等式两边则分别表示了资产 i 和其他资产的，相对于理论数量的差值*各自价格，即 价值的变量是相等的
       • 将等式变形就能求出资产 i 的新价格 p_i
   • tweak_price(A_gamma, xp, ix, p, D)
     • 会根据 repeg 逻辑更新D, virtual_price, xcp_profit，以及 price_scale_packed, last_prices_packed
     • 只有当前有足够的利润时才会改变价格 price_scale

计算价格的逻辑

• 当用户按照当前池子资产的比例添加流动性时，不会引起资产比例的变化，此时可以认为没有发生交易
• 而当用户不按照比例添加，比如只添加单一资产，那么可以认为用户在平衡的添加流动性之后，做了一笔不完整的交易，改变了池子的资产比例
• 例如添加单一资产 i，mint 出 lp token 数量 d_token
  • 先假设用户按照原有比例添加流动性，那么每种资产的增加价值就可以通过 LP token 的增加比例计算 xp * (d_token / token_supply)
  • 然后假设用户做了一笔交易，增加了资产 i，而提走本应该增加的其他资产部分
  • 交易输入的价值 $p_i(amount_{in} - b_i\frac{dToken}{TotalSupply})$
  • 交易输出的价值 $\sum_{k\neq{i}}{p_k b_k \frac{dToken}{TotalSupply}}$
  • 交易输入和输出两个价值应该相等，由此可列等式求得 p_i
  • 上述计算不需要使用牛顿法求解，因此节省了 2 次 牛顿法求解 的开销，具体细节可以查看 tweak_price() 中涉及 newton_y() 的部分
• 如果添加资产是 1 种以上，进入 tweak_price 时将带入参数 p = 0，即在 tweak_price 中使用 newton_y() 计算交易输出量，然后计算出交易的价格，便于后续的 repegging 逻辑。

@external
@nonreentrant('lock')
def add_liquidity(amounts: uint256[N_COINS], min_mint_amount: uint256):
    assert not self.is_killed  # dev: the pool is killed

    A_gamma: uint256[2] = self._A_gamma()

    _coins: address[N_COINS] = coins

    xp: uint256[N_COINS] = self.balances    # xp container, cache balances first, will multiply price later
    amountsp: uint256[N_COINS] = empty(uint256[N_COINS])
    xx: uint256[N_COINS] = empty(uint256[N_COINS])          # another xp container, cache balances
    d_token: uint256 = 0            # the amount of LP-token that will be minted
    d_token_fee: uint256 = 0        # fees of mint
    old_D: uint256 = 0              # cache D value
    ix: uint256 = INF_COINS         # the index of asset that has increment

    if True:
        xp_old: uint256[N_COINS] = xp

        # calculate balances after add liquidity
        for i in range(N_COINS):
            bal: uint256 = xp[i] + amounts[i]
            xp[i] = bal
            self.balances[i] = bal
        xx = xp

        precisions: uint256[N_COINS] = PRECISIONS           # unify the decimal of tokens
        packed_prices: uint256 = self.price_scale_packed
        xp[0] *= PRECISIONS[0]      # xp after add liquidity
        xp_old[0] *= PRECISIONS[0]  # xp before add liquidity
        for i in range(1, N_COINS): # calculate value of assets, xp = balance * price
            price_scale: uint256 = bitwise_and(packed_prices, PRICE_MASK) * precisions[i]  # * PRICE_PRECISION_MUL
            xp[i] = xp[i] * price_scale / PRECISION
            xp_old[i] = xp_old[i] * price_scale / PRECISION
            packed_prices = shift(packed_prices, -PRICE_SIZE)

        # Transfer incremental assets into contracts in turn
        # ix's logic as follows：
        # INF_COINS = 15, it means no incremental asset.
        # If only one incremental asset, ix will be the index of the incremental asset
        #   At this time, price changes, the transaction price will be calculated and pass to tweak_price()
        # If there are multiple incremental assets, ix will be INF_COINS-1 = 14，now zero will pass to tweak_price()
        #   as price ， then recalculate price in tweak_price

        for i in range(N_COINS):
            if amounts[i] > 0:
                # assert might be needed for some tokens - removed one to save bytespace
                ERC20(_coins[i]).transferFrom(msg.sender, self, amounts[i])
                amountsp[i] = xp[i] - xp_old[i]
                if ix == INF_COINS:
                    ix = i
                else:
                    ix = INF_COINS-1
        assert ix != INF_COINS  # If IX does not change, there is no incremental asset and the transaction is terminated

        t: uint256 = self.future_A_gamma_time
        if t > 0:
            old_D = Math(math).newton_D(A_gamma[0], A_gamma[1], xp_old)
            if block.timestamp >= t:
                self.future_A_gamma_time = 1
        else:
            old_D = self.D

    D: uint256 = Math(math).newton_D(A_gamma[0], A_gamma[1], xp)        # calc D after add liquidity

    token_supply: uint256 = CurveToken(token).totalSupply()             # cache LP token_supply
    # If there is liquidity already, scale totalSupply by D，then calc d_token as mint amount
    if old_D > 0:
        d_token = token_supply * D / old_D - token_supply
    # If add liquidity first time, d_token will be Xcp, then the virtual_price will be 1
    else:
        d_token = self.get_xcp(D)
    assert d_token > 0  # dev: nothing minted

    # Adding liqudity imbalanced is also an exchanging，so we will call tweak_price function to do repegging.
    # Need pass price p to tweak_price function, if p is zero, tweak_price will recalculate price.
    # p can be directly calculated if the following conditions are met
    #   1. D > 0
    #   2. d_token > min_amount after cost fees
    # otherwise recalculate it in twaek_price.
    if old_D > 0:
        d_token_fee = self._calc_token_fee(amountsp, xp) * d_token / 10**10 + 1
        d_token -= d_token_fee
        token_supply += d_token
        CurveToken(token).mint(msg.sender, d_token)

        # Calculate price
        # p_i * (dx_i - dtoken / token_supply * xx_i) = sum{k!=i}(p_k * (dtoken / token_supply * xx_k - dx_k))
        # Only ix is nonzero
        p: uint256 = 0
        if d_token > 10**5:     # (10**5 is very small compared to 10**18)
            if ix < N_COINS:
                S: uint256 = 0
                last_prices: uint256[N_COINS-1] = empty(uint256[N_COINS-1])
                packed_prices: uint256 = self.last_prices_packed
                precisions: uint256[N_COINS] = PRECISIONS
                for k in range(N_COINS-1):
                    last_prices[k] = bitwise_and(packed_prices, PRICE_MASK)  # * PRICE_PRECISION_MUL
                    packed_prices = shift(packed_prices, -PRICE_SIZE)
                for i in range(N_COINS):
                    if i != ix:
                        if i == 0:
                            S += xx[0] * PRECISIONS[0]      # coin[0]'s price is always 1
                        else:
                            S += xx[i] * last_prices[i-1] * precisions[i] / PRECISION
                # S = sum{k!=i}(p_k * (dtoken / token_supply * xx_k - dx_k))
                # dx_k can be omitted, because only asset i added
                S = S * d_token / token_supply
                p = S * PRECISION / (amounts[ix] * precisions[ix] - d_token * xx[ix] * precisions[ix] / token_supply)

        # call tweak_price function, do reppeging
        self.tweak_price(A_gamma, xp, ix, p, D)

    else:       # add liquidity first time, there is no need to calculate price
        self.D = D
        self.virtual_price = 10**18
        self.xcp_profit = 10**18
        CurveToken(token).mint(msg.sender, d_token)

    assert d_token >= min_mint_amount, "Slippage"

    log AddLiquidity(msg.sender, amounts, d_token_fee, token_supply)

remove_liquidity

移除流动性，赎回资产将按照池子当前的比例返还。

1. 销毁用户的 LP token
2. 根据移除的 LP token 数量和 totalSupply 的比例，同比计算每种资产的赎回数量，转账资产给用户
3. 根据该比例，同比减少 D

@external
@nonreentrant('lock')
def remove_liquidity(_amount: uint256, min_amounts: uint256[N_COINS]):
    """
    This withdrawal method is very safe, does no complex math
    """
    _coins: address[N_COINS] = coins
    total_supply: uint256 = CurveToken(token).totalSupply()
    CurveToken(token).burnFrom(msg.sender, _amount)
    balances: uint256[N_COINS] = self.balances
    amount: uint256 = _amount - 1  # round up, small for LP, but safe for division

    for i in range(N_COINS):
        d_balance: uint256 = balances[i] * amount / total_supply
        assert d_balance >= min_amounts[i]
        self.balances[i] = balances[i] - d_balance
        balances[i] = d_balance  # now it's the amounts going out
        # assert might be needed for some tokens - removed one to save bytespace
        ERC20(_coins[i]).transfer(msg.sender, d_balance)

    D: uint256 = self.D
    self.D = D - D * amount / total_supply

    log RemoveLiquidity(msg.sender, balances, total_supply - _amount)

remove_liquidity_one_coin

移除流动性只收取单一资产,由于移除资产比例不平衡，将产生交易手续费

@external
@nonreentrant('lock')
def remove_liquidity_one_coin(token_amount: uint256, i: uint256, min_amount: uint256):
    assert not self.is_killed  # dev: the pool is killed

    A_gamma: uint256[2] = self._A_gamma()

    dy: uint256 = 0
    D: uint256 = 0
    p: uint256 = 0
    xp: uint256[N_COINS] = empty(uint256[N_COINS])
    future_A_gamma_time: uint256 = self.future_A_gamma_time

    # Calc amount of assets after remove liquidity
    # If A is ramping, need to recalculate D with the ramping A
    dy, p, D, xp = self._calc_withdraw_one_coin(A_gamma, token_amount, i, (future_A_gamma_time > 0), True)
    assert dy >= min_amount, "Slippage"

    # If A's changing end, set future_A_gamma_time to 1, so that call tweak_price again, will set it to zero
    if block.timestamp >= future_A_gamma_time:
        self.future_A_gamma_time = 1

    # Update balances, burn LP token, transfer unlying token to provider
    self.balances[i] -= dy
    CurveToken(token).burnFrom(msg.sender, token_amount)
    _coins: address[N_COINS] = coins
    # assert might be needed for some tokens - removed one to save bytespace
    ERC20(_coins[i]).transfer(msg.sender, dy)

    # Call tweak_price because some exchanging happened in remove liquidity
    self.tweak_price(A_gamma, xp, i, p, D)


    log RemoveLiquidityOne(msg.sender, token_amount, i, dy)

Difference from v1 Remove

Curve V2 CryptoSwap 在移除流动性上有一点与 v1 不同，即没有提供 StableSwap#remove_liquidity_imbalance 接口。流动性提供者不再可以设置任意的移除比例（比如 1:2:3），而只有两种选择：

• remove_liquidity_one_coin 移除流动性得到单一底层资产
• remove_liquidity 移除流动性，得到三种资产，其比例按照池子内当时的总比例分配

对于不平衡的添加/移除流动性，Curve 将其定义为一种不完整的交易，所以需要对部分收取手续费，其计算逻辑我们将在下一章展开。