Curve newton's method (CN)|Curve|code review • 0xreviews.xyz

curve V1&V2 牛顿法代码思路及借鉴创新-(对 curve math 库做科普)

1. 牛顿法在 solidity&vyper 的必要性和重要性

像互联网走过的 web1.0，web2.0 之路时，最终捕获最大价值的是面向用户的应用层一样。区块链世界并不缺少越发同质化基础设施,缺少的是各种功能不同的应用层。如果 web3.0 之路真的在未来大行其道，那么捕获价值的推手将由目前的基础层转向应用层。笔者认为，目前的 EVM 的性能瓶颈和运算 gas 消耗加上 solidity, vyper 的一些语言特性让很多开发者目前对很多应用功能是望而却步的，其中数值计算的性能-资源消耗之间的不平衡正是目前开发者面临的一个比较头疼的问题。很多在 python,C++,Javascript 中“快”和“省”的算法用 solidity, vyper 实现不得不做出各种变形妥协。甚至很多项目方为了实现特定的函数功能，需要单独实现一个很难理解的算法功能，而这些实现的算法却很难成为一个万能的轮子供其他开发者直接使用，理解这些算法需要开发者们一同努力。

Curve 正是上文提到的这类项目方，它是典型的由单个开发者主导的具有非常多原创 idea 和工程实现创新的项目，Curve 在区块链世界重要性无需赘述。

我们在这里向伟大的 Curve 创始人 Michael Egorov 致敬，感谢他在区块链带来的各种创新，本文就其中一小点，提出自己的看法和见解，目的有三：

科普 Curve 项目中的牛顿算法
对牛顿算法在不同业务场景中进行的变形方法和思路。
抛砖引玉启发后人对其他数值优化算法的研究

第三点是笔者认为的最重要的事情，原因如下：

显然经典牛顿法并不是数值优化最快和最省的万能算法，正如没有 1 个 defi 项目敢保证自己没有任何漏洞一样，defi 世界也不存在 1 个数值优化算法能保证他在该项目中最“快”且最“省”。本文希望后续的研究者们能对我们提出的问题继续深入的研究和探讨，问题如下（如果可能的话，我们想请 Curve 项目授予以下问题 Grant 支持）：

如何完整的证明 Curve 中的放缩改进过的牛顿法一定是收敛的（不收敛会带来灾难后果）。
Curve 的牛顿法若不是最优有其他更好算法替代，哪种算法是最“快”最“省”的（省 gas）。
对牛顿法或者牛顿法的变种造个 solidity 函数轮子，满足其他大部分开发者的基本数值计算需求（省开发者头发）。

2. 牛顿法在 Curve v1 的代码实现思路

vyper合约中相关部分的注释和代码不一致，这里放上我们的文章链接：

https://0xreviews.xyz/2022/02/12/Curve-v1-StableSwap/#d

2.1 牛顿法科普

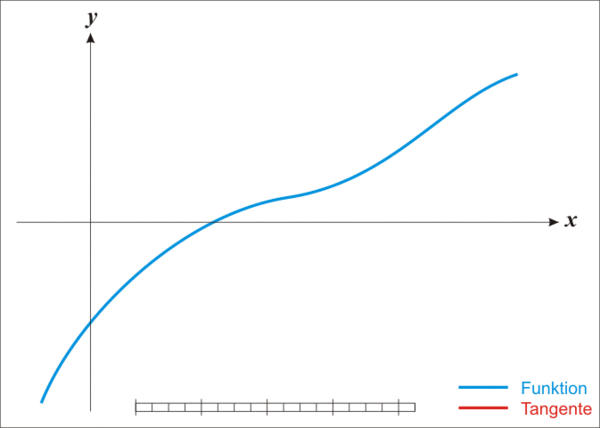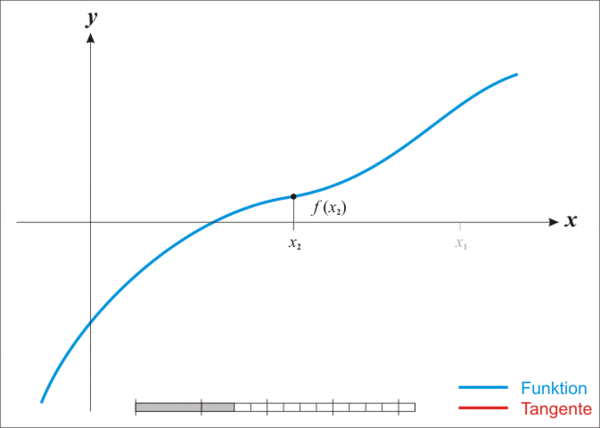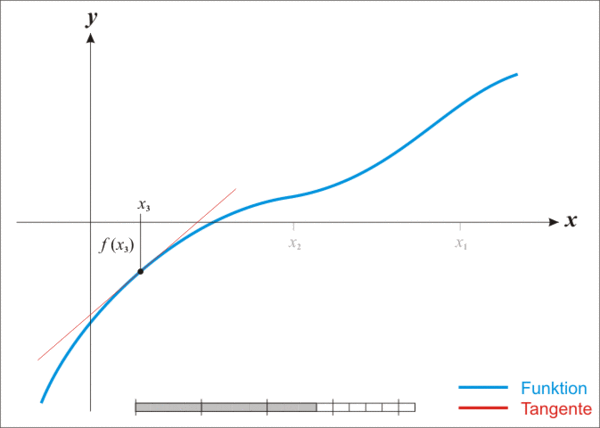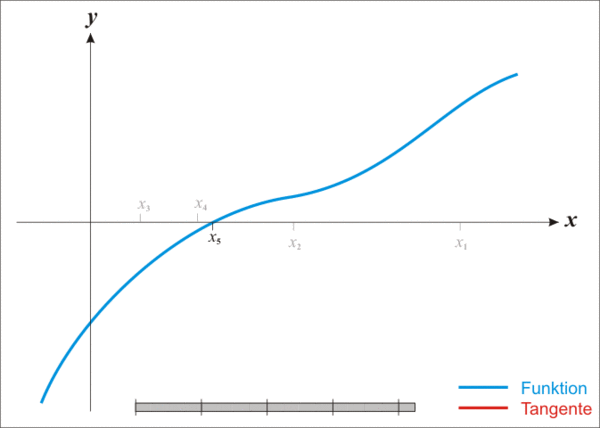
由于智能合约中不能直接解方程，curve 在合约中使用了牛顿法迭代求近似解。

$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$

简单理解牛顿法就是利用上述公式，不断迭代 x_n+1 的值，使其越来越逼近真实的解

2.2 Curve V1——函数 get_D 的牛顿法推导过程及对应代码

代码中使用的牛顿法的函数 f(D)，是用核心公式推导得来，下面简述推导过程：

首先将核心公式变形成 f(D) = 0 的形式

$f(D)=An^n\Sigma x_i + D-ADn^n-\frac{D^{n+1}}{n^n\Pi x_i}$
D_new = D - f(D)/f'(D)

$D_{new}=D-\frac{An^n\Sigma x_i + D-ADn^n-\frac{D^{n+1}}{n^n\Pi x_i}}{1-An^n-(n+1)\frac{D^n}{n^n\Pi x_i}}$
最终变成代码中的形态

$D_{new}=\frac{An^n\Sigma x_i-\frac{D^{n+1}}{n^n\Pi x_i}}{An^n+(n+1)\frac{D^n}{n^n\Pi x_i}-1}$
for 循环迭代求 D 的解，当迭代到 D 与上一次的差值 <= 1 时，停止迭代；
通常轮迭代不超过 4 轮就会找到最优解；但如果迭代 255 次仍然没有找到合适的解，程序终止，交易回滚 (revert)；用户可以通过 remove_liquidity 方法回收资产；

注意：注释中的牛顿法公式写漏了一项，而代码写的是正确的化简后的公式。

curve-contract SwapTemplateBase.vy#L214

@pure
@internal
def _get_D(_xp: uint256[N_COINS], _amp: uint256) -> uint256:
    """
    D invariant calculation in non-overflowing integer operations
    iteratively

    A * sum(x_i) * n**n + D = A * D * n**n + D**(n+1) / (n**n * prod(x_i))

    Converging solution:
    D[j+1] = (A * n**n * sum(x_i) - D[j]**(n+1) / (n**n prod(x_i))) / (A * n**n + (n+1)*D[j]**n/(n**n prod(x_i)) - 1)

    这里原版代码注释分母漏掉了一项
    (n+1)*D[j]**n/(n**n prod(x_i))

    原版代码链接:
    https://github.com/curvefi/curve-contract/blob/master/contracts/pool-templates/base/SwapTemplateBase.vy#L214
    """
    S: uint256 = 0
    Dprev: uint256 = 0

    for _x in _xp:
        S += _x
    if S == 0:
        return 0

    D: uint256 = S
    Ann: uint256 = _amp * N_COINS
    for _i in range(255):
        D_P: uint256 = D
        for _x in _xp:
            D_P = D_P * D / (_x * N_COINS)  # If division by 0, this will be borked: only withdrawal will work. And that is good
            # 只有当移除流动性时才有可能 _x 为0，这时程序会崩溃，这也是期望的结果
            # 添加流动性，池内的xp值不可能为0
        Dprev = D
        D = (Ann * S / A_PRECISION + D_P * N_COINS) * D / ((Ann - A_PRECISION) * D / A_PRECISION + (N_COINS + 1) * D_P)
        # Equality with the precision of 1
        # 当迭代的新值和上次之差，小于等于 1，即0或1
        # 认为找到了局部最优解
        if D > Dprev:
            if D - Dprev <= 1:
                return D
        else:
            if Dprev - D <= 1:
                return D
    # convergence typically occurs in 4 rounds or less, this should be unreachable!
    # if it does happen the pool is borked and LPs can withdraw via `remove_liquidity`
    raise


@view
@internal
def _get_D_mem(_balances: uint256[N_COINS], _amp: uint256) -> uint256:
    return self._get_D(self._xp_mem(_balances), _amp)

2.3 在 Curve Team 关于 get_D 的历史错误上更进一步探究、创新和总结

从错误中学习正确的牛顿法思路。我们在对基于 vyper 的 Curve 进行 solidity 重构时发现了此处的注释和源码不一致(在 Curve 源码中注释的缺失和错误是比较常见的)。

注释是 Sam Werner 先写的，Sam Werner 是 Curve team 成员,He is a PhD student in the Centre for Cryptocurrency Research and Engineering at Imperial。我们当时认为帝国理工同样 Phd 出身的 Sam 在这里可能提出的是相较 Curve CEO 更好的一个方法，所以写在了注释中。所以我们按照 saw 的方法写出来了一种牛顿法，此次篇幅所限不再展开，

按照 saw 的注释思路，不改变牛顿法的分子，通过对分母进行放缩化简之后改变的是牛顿法每次切线的斜率。理论上是能输出同样的数值结果。

最后的实验结果是：改变分母也就是牛顿法的切线斜率并不会是最终的结果产生太大的偏移。但是会很大程度上影响牛顿法的收敛性。我们知道 Curve V1 和 V2 中的牛顿法都需要在 255 次运算内完成特定精度（这个上限很难触及，因为gas可能早已耗尽）。

关于牛顿法的收敛性：牛顿法的全局收敛性的结论也是在 2018 年才被证明。牛顿法在靠近最优点处是二次收敛的，结论为牛顿法下，函数只需要最多 $log log (1/\varepsilon)$ 步就能够使得得到的最优化近似解与实际最优点之间的距离小于 $\varepsilon$ ,Defi 的常用精度为 10^18， $log log (1/10^-18)$ 计算可知结果约为 4，这也是作者所说的。大部分牛顿法在 4 次左右可以得到结果的理论的依据。

实验结果证明改变牛顿法的斜率会验证破坏牛顿法收敛速度，使得牛顿法处于实际不可用状态。

牛顿法有以下几种衍生出来的方法，包括牛顿法的直接改进（AN HN MN），阻尼牛顿法和拟牛顿法（DFP、BFGS、L-BFGS），这些算法相对于直接放缩牛顿法中的导数是更为安全的算法。直接对牛顿法的放缩是一个较少经过验证的方法。我们也考虑了在 Curve V2 中进行部分放缩，同样发现结果收敛速度不太理想。

总而言之，这里的确 Sam Werner 是给了一个不太好的注释，却意外的启发了我们对牛顿法更加深刻的理解和运用。

2.4 Curve V1——函数 get_y 的牛顿法推导过程及对应代码

输入资产 i ，变化之后的数量 x，变化之前的 _xp，计算输出资产 j 变化后的数量。

与计算 D 一样，这里也使用了牛顿法计算 y, 即 x_j，其 f(x_j) 推导过程如下：

$An^n\sum{x_i} + D = ADn^n + \frac{D^{n+1}}{n^n\prod x_i}$

设 sum', prod' 分别为排除输出资产数量的累加和累乘结果
- sum' = sum(x) - x_j
- prod' = prod(x) / x_j
核心公式除以 A*n**n

$\sum{x_i}+\frac{D}{An^n}-D=\frac{D^{n+1}}{An^nn^n\prod x_i}$
乘以 x_j，并代入 sum' 和 prod'

$x_j(x_j+sum')-x_j(An^n-1)\frac{D}{An^n}=\frac{D^{n+1}x_j}{An^{2n}(prod'*x_j)}$
展开多项式，即为牛顿法使用的 f(x_j)

$x_j^2+x_j(sum'-(An^n-1)\frac{D}{An^n})=\frac{D^{n+1}}{An^{2n}prod'}$
将其写为 x_j**2 + b*x_j = c 形式，代入牛顿法公式 x = x - f(x) / f'(x)
- x_j = (x_j**2 + c) / (2*x_j + b)

@view
@internal
def _get_y(i: int128, j: int128, x: uint256, _xp: uint256[N_COINS]) -> uint256:
    """
    Calculate x[j] if one makes x[i] = x

    Done by solving quadratic equation iteratively.
    x_1**2 + x_1 * (sum' - (A*n**n - 1) * D / (A * n**n)) = D ** (n + 1) / (n ** (2 * n) * prod' * A)
    x_1**2 + b*x_1 = c

    x_1 = (x_1**2 + c) / (2*x_1 + b)
    """
    # x in the input is converted to the same price/precision

    assert i != j       # dev: same coin
    assert j >= 0       # dev: j below zero
    assert j < N_COINS  # dev: j above N_COINS

    # should be unreachable, but good for safety
    assert i >= 0
    assert i < N_COINS

    A: uint256 = self._A()
    D: uint256 = self._get_D(_xp, A)
    Ann: uint256 = A * N_COINS
    c: uint256 = D
    S: uint256 = 0
    _x: uint256 = 0
    y_prev: uint256 = 0

    for _i in range(N_COINS):
        if _i == i:
            _x = x
        elif _i != j:
            _x = _xp[_i]
        else:
            continue
        S += _x
        c = c * D / (_x * N_COINS)
    c = c * D * A_PRECISION / (Ann * N_COINS)
    b: uint256 = S + D * A_PRECISION / Ann  # - D
    y: uint256 = D
    for _i in range(255):
        y_prev = y
        y = (y*y + c) / (2 * y + b - D)
        # Equality with the precision of 1
        if y > y_prev:
            if y - y_prev <= 1:
                return y
        else:
            if y_prev - y <= 1:
                return y
    raise


@view
@external
def get_dy(i: int128, j: int128, _dx: uint256) -> uint256:
    xp: uint256[N_COINS] = self._xp()
    rates: uint256[N_COINS] = RATES

    x: uint256 = xp[i] + (_dx * rates[i] / PRECISION)
    y: uint256 = self._get_y(i, j, x, xp)
    dy: uint256 = xp[j] - y - 1
    fee: uint256 = self.fee * dy / FEE_DENOMINATOR
    return (dy - fee) * PRECISION / rates[j]

还有个 _get_y_D() 函数，与上述区别是可以自定义 D 的值来求 y

@pure
@internal
def _get_y_D(A: uint256, i: int128, _xp: uint256[N_COINS], D: uint256) -> uint256:

3. 牛顿法在 Curve v2 中代码实现思路

Curve V2 中的牛顿法存在一定的变形，在注释不充分前提下，相对来说更难充分理解。在这里我们介绍牛顿法时，忽略掉技术细节。我们在此处直接从作者的角度来看，他是如何一步讲数学思想转换得到代码，希望能够启发后人设计更加复杂的算法。在这里为了方便更好的进行理解，我们展示的代码为 Python 版本的测试文件中的代码。

https://github.com/curvefi/curve-crypto-contract/blob/master/tests/simulation_int_many.py

3.1 Curve V2—函数 geometric_mean 的牛顿法推导过程及对应代码

这里是输入数组 x 求其几何平均值为 D，我们将代码中 D 记作 d，N 记作 n，如公式所示:

$d=\left(\prod _{i=0}^{n-1} x(i)\right){}^{1/n}$

d 是牛顿法求解目标，为了对构造的函数更好的求导，等式 2 边同时放大 n 次方得到

$d^n=\prod _{i=0}^{n-1} x(i)$

方程右边移到左边构造函数为 f(d)

$f(d)=d^n-\prod _{i=0}^{n-1} x(i)$

对 f(d)求导

$f'(d)=n d^{n-1}$

根据牛顿法 d_new= d_prev-f(d_prev)/f'(d_prev)

$d_{\text{new}}=d-\frac{d^n-\prod _{i=0}^{n-1} x(i)}{n d^{n-1}}$

去掉分母中的 $(d^{n-1})$ ,得到

$d_{\text{new}}=d-\frac{d-\frac{\prod _{i=0}^{n-1} x(i)}{d^{n-1}}}{n}$

接下来需要把将方程变成分子/分母形式，这样方便先在分子中进行化简，使用先乘后除原则有利于 vyper&solidity 的整除控制精度。

$d_{\text{new}}=\frac{nd-d+\frac{\prod _{i=0}^{n-1} x(i)}{d^{n-1}}}{n}$

出现了 $\frac{\prod _{i=0}^{n-1} x(i)}{d^{n-1}}$ ，分子为关于 n 次项，分母为关于 d 的 n-1 次项，为了分子分母都为 n 此项以便于代码迭代时讲二者同时迭代，我们自然而然想到要将此处函数变成同样为 n 次的，给分子和分母同时乘以 d

$d_{\text{new}}=\frac{nd-d+\frac{d \left(\prod _{i=0}^{n-1} x(i)\right)}{d^n}}{n}$

然后对分子进行化简，提取公因数 d，这样化简优化了计算消耗。

$d_{\text{new}}=\frac{d \left((n-1)+\frac{\prod _{i=0}^{n-1} x(i)}{d^n}\right)}{n}$

至此我们看到代码中

D = D * ((N - 1) * 10 ** 18 + tmp) // (N * 10**18)

由来已经水落石出。其中 tmp 正是我们推导变形时候考虑到的 $\frac{\prod _{i=0}^{n-1} x(i)}{d^{n}}$ ，刚好和进行 n 次 for 循环得到的 tmp 对应起来。加上精度控制之后刚好和作者代码一致。


def geometric_mean(x):
    N = len(x)
    x = sorted(x, reverse=True)  # Presort - good for convergence
    D = x[0]
    for i in range(255):
        D_prev = D
        tmp = 10 ** 18
        for _x in x:
            tmp = tmp * _x // D
        D = D * ((N - 1) * 10**18 + tmp) // (N * 10**18)
        diff = abs(D - D_prev)
        if diff <= 1 or diff * 10**18 < D:
            return D
    print(x)
    raise ValueError("Did not converge")

3.2 Curve V2—函数 newton_D 的牛顿法推导过程及对应代码

白皮书中公式如下,牛顿法的初值为 D0

平衡方程： $KD^{N-1}{\Large\sum}{x_i}+{\Large\prod} x_i=KD^N+\left(\dfrac{D}{N}\right)^N$

$K_0 = \dfrac{\prod x_iN^N}{D^N}$ , $K=AK_0\dfrac{\gamma^2}{(\gamma+1-K_0)^2}$

$F(x,D)=K(x,D)D^{N-1}{\Large\sum}{x_i}+{\Large\prod}(x_i)-K(x,D)D^N-\left(\dfrac{D}{N}\right)^N$

$D_0=N\left({\Large\prod}x_k\right)^{\frac{1}{N}}$

作者是如何想到的牛顿法的呢，其中 mul1 和 mul2 这些中间变量为何存在，我们以 d 替换 D 进行推导按照作者思路：首先完全展开 Curve V2 的平衡方程

$f(d)=-\frac{A \gamma ^2 n^n \prod _{i=1}^n x(i)}{\left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^2}+\frac{A \gamma ^2 n^n \left(\prod _{i=1}^n x(i)\right) \sum _{i=1}^n x(i)}{d \left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^2}+\prod _{i=1}^n x(i)-\left(\frac{d}{n}\right)^n$

上式对 d 求导：

$f'(d)=\frac{2 A \gamma ^2 n^{2 n+1} d^{-n-1} \left(\prod _{i=1}^n x(i)\right){}^2}{\left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^3}-\frac{2 A \gamma ^2 n^{2 n+1} d^{-n-2} \left(\prod _{i=1}^n x(i)\right){}^2 \left(\sum _{i=1}^n x(i)\right)}{\left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^3}-\frac{A \gamma ^2 n^n \left(\prod _{i=1}^n x(i)\right) \sum _{i=1}^n x(i)}{d^2 \left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^2}-\left(\frac{d}{n}\right)^{n-1}$

由牛顿法可知：

$d_{new}=d-f(d)/f'(d)$

展开得到：

$d_{new}=d-\frac{-\frac{A \gamma ^2 n^n \prod _{i=1}^n x(i)}{\left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^2}+\frac{A \gamma ^2 n^n \left(\prod _{i=1}^n x(i)\right) \sum _{i=1}^n x(i)}{d \left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^2}+\prod _{i=1}^n x(i)-\left(\frac{d}{n}\right)^n}{\frac{2 A \gamma ^2 n^{2 n+1} d^{-n-1} \left(\prod _{i=1}^n x(i)\right){}^2}{\left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^3}-\frac{2 A \gamma ^2 n^{2 n+1} d^{-n-2} \left(\prod _{i=1}^n x(i)\right){}^2 \left(\sum _{i=1}^n x(i)\right)}{\left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^3}-\frac{A \gamma ^2 n^n \left(\prod _{i=1}^n x(i)\right) \sum _{i=1}^n x(i)}{d^2 \left(-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1\right){}^2}-\left(\frac{d}{n}\right)^{n-1}}$

分母出现较多的为 $-n^n d^{-n} \left(\prod _{i=1}^n x(i)\right)+\gamma +1$ ,这是平衡方程中 $\gamma+1-K_0$ 的展开式。方便观察化简，我们将 $\gamma+1-K_0$ 记作 g1k0 替换后方程变为：

$d-\frac{\frac{A \gamma ^2 n^n \left(\prod _{i=1}^n x(i)\right) \sum _{i=1}^n x(i)}{d\ \text{g1k0}^2}-\frac{A \gamma ^2 n^n \prod _{i=1}^n x(i)}{\text{g1k0}^2}+\prod _{i=1}^n x(i)-\left(\frac{d}{n}\right)^n}{\frac{2 A \gamma ^2 n^{2 n+1} d^{-n-1} \left(\prod _{i=1}^n x(i)\right){}^2}{\text{g1k0}^3}-\frac{2 A \gamma ^2 n^{2 n+1} d^{-n-2} \left(\prod _{i=1}^n x(i)\right){}^2 \left(\sum _{i=1}^n x(i)\right)}{\text{g1k0}^3}-\frac{A \gamma ^2 n^n \left(\prod _{i=1}^n x(i)\right) \sum _{i=1}^n x(i)}{d^2 \text{g1k0}^2}-\left(\frac{d}{n}\right)^{n-1}}$

同时将 $\prod _{i=1}^n x(i)$ 简写为 Prod,将 $\sum _{i=1}^n x(i)$ 简写为 S，上述方程化简为：

$d-\frac{\frac{A \gamma ^2 n^n \text{Prod} S}{d \text{g1k0}^2}-\frac{A \gamma ^2 n^n \text{Prod}}{\text{g1k0}^2}-\left(\frac{d}{n}\right)^n+\text{Prod}}{\frac{2 A \gamma ^2 n^{2 n+1} \text{Prod}^2 d^{-n-1}}{\text{g1k0}^3}-\frac{2 A \gamma ^2 n^{2 n+1} \text{Prod}^2 S d^{-n-2}}{\text{g1k0}^3}-\frac{A \gamma ^2 n^n \text{Prod} S}{d^2 \text{g1k0}^2}-\left(\frac{d}{n}\right)^{n-1}}$

将分子和分母分别记作：

$\text{numerator}=\frac{A \gamma ^2 n^n \text{Prod} S}{d \text{g1k0}^2}-\frac{A \gamma ^2 n^n \text{Prod}}{\text{g1k0}^2}-\left(\frac{d}{n}\right)^n+\text{Prod}$

$\text{denominator}=\frac{2 A \gamma ^2 n^{2 n+1} \text{Prod}^2 d^{-n-1}}{\text{g1k0}^3}-\frac{2 A \gamma ^2 n^{2 n+1} \text{Prod}^2 S d^{-n-2}}{\text{g1k0}^3}-\frac{A \gamma ^2 n^n \text{Prod} S}{d^2 \text{g1k0}^2}-\left(\frac{d}{n}\right)^{n-1}$

接下来我们对该复杂式子进行观察分析，可以看到该分子分母大部分项含有 $\frac{A \gamma ^2 n^n \text{Prod}}{\text{g1k0}^2}$ 作为公因子。而在平衡方程中的 $K=\frac{A \gamma ^2 n^n d^{-n} \text{Prod}}{\text{g1k0}^2}$ 可以看到与该因子非常像。而且 K 本身含有 K0，而 K0 包含了 N 次循环且含有 D。因此将 K 作为一个新的公因数强行提出可以得到：

$denominator= \frac{A \gamma ^2 n^n d^{-n} \text{Prod}}{\text{g1k0}^2}*(-\frac{\text{g1k0}^2 n^{1-n} d^{n-1}}{A \gamma ^2 n^n \text{Prod}}-\frac{2 n^{n+1} \text{Prod} S d^{-n-2}}{\text{g1k0}}+\frac{2 n^{n+1} \text{Prod} d^{-n-1}}{\text{g1k0}}-\frac{S}{d^2})$

我们发现在 denominator 中出现 $\text{Prod}*n^n d^{-n}=K0$ 这一因子，我们将对 denominator 中类似 K0 结构式子转换为 K0 进行化简：

$denominator= K*(-\frac{\text{g1k0}^2 n}{d \left(A \gamma ^2 \text{K0} n^n\right)}-\frac{2 \text{K0} n S}{d^2 \text{g1k0}}-\frac{S}{d^2}+\frac{2 \text{K0} n}{d \text{g1k0}})$

然后我们观察分母含有 $d$ ，我们考虑消去分母。同时注意到 $A$ 和 $n^n$ 一直同时出现，将 $An^n$ 合并记作 ANN。得到下式：

$denominator= Kd^2*(-\frac{d \text{g1k0}^2 n}{ANN \gamma ^2 \text{K0} }+\frac{2 d \text{K0} n}{\text{g1k0}}-\frac{2 \text{K0} n S}{\text{g1k0}}-S)$

再次观察，我们发现式子较多含有 $\frac{2 \text{K0} n }{\text{g1k0}}$ 我们将其标记为 mul2,同时将第一项较为复杂式子中不涉及 K0 及 for 循环的部分剥离记作 $mul1=d*\frac{\text{g1k0}^2}{\text{ANN} \gamma ^2}$

$denominator=-Kd^2(S+S * {mul2}+ {mul1} \frac{n}{K0} - {mul2}*d)$

记-denominator/Kd^2 为 neg_prime 同理对分子提出 Kd^2 进行变形可得类似结果带入以下式子可得：

$d_{new}=d-f(d)/f'(d)$

$d_{new} = (d * \text{neg\_fprime} + d * S - d^2)/\text{neg\_fprime} - d * ({mul1}/\text{neg\_fprime}) * (1-K0)/ K0$

得到了和代码中一模一样的核心牛顿公式。


def newton_D(A, gamma, x, D0):
    D = D0
    i = 0

    S = sum(x)
    x = sorted(x, reverse=True)
    N = len(x)

    for i in range(255):
        D_prev = D

        K0 = 10**18
        for _x in x:
            K0 = K0 * _x * N // D

        _g1k0 = abs(gamma + 10**18 - K0)

        # D / (A * N**N) * _g1k0**2 / gamma**2
        mul1 = 10**18 * D // gamma * _g1k0 // gamma * _g1k0 * A_MULTIPLIER // A

        # 2*N*K0 / _g1k0
        mul2 = (2 * 10**18) * N * K0 // _g1k0

        neg_fprime = (S + S * mul2 // 10**18) + mul1 * N // K0 - mul2 * D // 10**18
        assert neg_fprime > 0  # Python only: -f' > 0

        # D -= f / fprime
        D = (D * neg_fprime + D * S - D**2) // neg_fprime - D * (mul1 // neg_fprime) // 10**18 * (10**18 - K0) // K0

        if D < 0:
            D = -D // 2
        if abs(D - D_prev) <= max(100, D // 10**14):
            return D

    raise ValueError("Did not converge")

3.2 Curve V2—函数 newton_y 的牛顿法推导过程及对应代码

$x_{i}$ 即 newton_y 函数所计算的 y，其初值如下定义，将较快的迭代出结果。

$x_{i,0}=\frac{D^{N}}{\prod_{k \neq i}{x_k}N^{N}}$

白皮书中 x_i,0 初值的定义有误，分子中的 D 的幂写成 N-1，分母中 N 的幂写成 N-1，应该都为 N，代码中已经修正正确

~~白皮书中错误的初值定义：~~ $x_{i,0}=\frac{D^{N-1}}{\prod_{k \neq i}{x_k}N^{N-1}}$

作者是如何想到的牛顿法的呢，其中 mul1 和 mul2 这些中间变量为何存在，我们继续导按照作者思路：

同理完全展开 Curve V2 的平衡方程，为了书写方便，我们假设 x(n)是未知等待 newton_y 方法求解的。

我们将平衡方程展开并以关于 $x(n)$ 的函数形式进行化简分析

$f(x(n))=-\frac{A \gamma ^2 n^n x(n) \prod _{k=1}^{n-1} x(k)}{\left(-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1\right){}^2}+ \\ \frac{A \gamma ^2 n^n \left(x(n) \prod _{k=1}^{n-1} x(k)\right) \left(\sum _{k=1}^{n-1} x(k)+x(n)\right)}{d \left(-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1\right){}^2}+x(n) \left(\prod _{k=1}^{n-1} x(k)\right)-\left(\frac{d}{n}\right)^n$

对 $f(x(n))$ 求导得:

$f'(x(n))= -\frac{A \gamma ^2 n^n \prod _{k=1}^{n-1} x(k)}{\left(-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1\right){}^2}+\frac{A \gamma ^2 n^n x(n) \left(\prod _{k=1}^{n-1} x(k)\right)}{d \left(-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1\right){}^2}+ \\\\ \frac{A \gamma ^2 n^n \left(\prod _{k=1}^{n-1} x(k)\right) \left(\sum _{k=1}^{n-1} x(k)+x(n)\right)}{d \left(-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1\right){}^2}- \\\\ \frac{2 A \gamma ^2 n^{2 n} d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right){}^2}{\left(-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1\right){}^3}+ \\\\ \frac{2 A \gamma ^2 n^{2 n} d^{-n-1} x(n) \left(\prod _{k=1}^{n-1} x(k)\right){}^2 \left(\sum _{k=1}^{n-1} x(k)+x(n)\right)}{\left(-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1\right){}^3}+\prod _{k=1}^{n-1} x(k)$

和 newton_D 同理我们也是在观察中发现进行一下替换能够极大的提高可阅读性。

将 $-n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right)+\gamma +1$ 记作 g1k0。

将 $A*n^n$ 记作 ANN

将 $\sum _{k=1}^{n-1} x(k)$ 记作 S

化简为：

$f'(x(n))=-\frac{2 \text{ANN} \gamma ^2 n^n d^{-n} x(n) \left(\prod _{k=1}^{n-1} x(k)\right){}^2}{\text{g1k0}^3}+ \\ \frac{2 \text{ANN} \gamma ^2 n^n d^{-n-1} x(n) \left(\prod _{k=1}^{n-1} x(k)\right){}^2 \left(\sum _{k=1}^{n-1} x(k)+x(n)\right)}{\text{g1k0}^3}+\frac{\text{ANN} \gamma ^2 x(n) \left(\prod _{k=1}^{n-1} x(k)\right)}{d \text{g1k0}^2}+ \\ \frac{\text{ANN} \gamma ^2 \left(\prod _{k=1}^{n-1} x(k)\right) \left(\sum _{k=1}^{n-1} x(k)+x(n)\right)}{d \text{g1k0}^2}-\frac{\text{ANN} \gamma ^2 \prod _{k=1}^{n-1} x(k)}{\text{g1k0}^2}+\prod _{k=1}^{n-1} x(k)$

和 newton_D 函数同理我们经过观察将 K 提出来,同时将 $\prod_{k=1}^{n-1} x(k)$ 记作 $Prod_i$ 得到以下式子：

$f'(x(n))=K \left(\frac{\text{g1k0}^2 n^{-n} d^n}{\text{ANN} \gamma ^2 x(n)}+\left(\frac{\frac{n^{-n} \text{S\_i} d^n}{x(n)}+2 n^{-n} d^n}{d}-\frac{n^{-n} d^n}{x(n)}+\frac{2 \text{Prod\_i} S}{d \text{g1k0}}-\frac{2 \text{Prod\_i}}{\text{g1k0}}\right)\right)$

我们注意到分子出现 $Prod\_i$ 较多，而 $Prod\_i*x(n)=Prod$ ，故我们将 $\frac{1}{x(n)}$ 提出来进行化简得到：

$f'(x(n))=\frac{K}{x(n)}(\frac{\text{g1k0}^2 n^{-n} d^n}{\text{ANN} \gamma ^2}+\frac{n^{-n} S d^n+2 n^{-n} d^n x(n)}{d}- \\ \frac{n^{-n} d^n x(n)}{d}+n^{-n} \left(-d^n\right)+\frac{2 \text{Prod} S}{d \text{g1k0}}-\frac{2 \text{Prod}}{\text{g1k0}})$

继续观察可以看到上式含有较多的 $d^nn^{-n}$ 结构统一提出后得到下式：

$f'(x(n))=\frac{\left(K n^{-n} d^n\right)}{x(n)} \left(\frac{\text{g1k0}^2}{\text{ANN} \gamma ^2}+\frac{2 \text{K0} S}{d \text{g1k0}}+\frac{x(n)+S}{d}-\frac{2 \text{K0}}{\text{g1k0}}-1\right)$

分母中含有较多的 d，我们将 $1/d$ 挪到括号外中可得：

$f'(x(n))=\frac{\left(K n^{-n} d^{n-1}\right)}{x(n)} \left(\frac{\text{g1k0}^2 d}{\text{ANN} \gamma ^2}+S+\frac{2 \text{K0} S}{ \text{g1k0}}+x(n)-\frac{2 \text{K0}d}{\text{g1k0}}-d\right)$

再次观察，我们发现式子较多含有 S 将系数合并后得到 $mul2=1+ \frac{2 \text{K0} }{\text{g1k0}}$ 我们将其标记为 mul2,同时将第一项较为复杂式子中不涉及 K0 及 for 循环的部分剥离记作 $mul1=d*\frac{\text{g1k0}^2}{\text{ANN} \gamma ^2}$

将 x(n)记作 newton_y 待求解的 y

$f'(x(n))=\frac{\left(K n^{-n} d^n\right)}y*(y + S * {mul2} + mul1 - D * mul2)$

记将上式括号中的部分记作为 yfprime

$\text{yfprime}=(y + S * mul2 + mul1 - D * mul2))$

而 fprime 则为

$\text{fprime}=\text{yfprime}/y$

可见和代码中的核心迭代一致

同理对分子提出 Kd^2 进行变形可得类似结果带入以下式子可得：

$y_{new}=y-f(y)/f'(y)$

$y_{new} = (\text{yfprime} + D - S) / \text{fprime} + mul1 / \text{fprime} * (1 - K0) / K0$

得到了和代码中一模一样的核心牛顿公式。


def newton_y(A, gamma, x, D, i):
    N = len(x)

    y = D // N      # 这里在进入for循环前，多乘了一次 D/N (白皮书中初值定义少了这个 D/N)
    K0_i = 10**18   # K0 的值
    S_i = 0
    x_sorted = sorted(_x for j, _x in enumerate(x) if j != i)           # 排除资产y的xp，对其他xp进行从小到大的排序
    convergence_limit = max(max(x_sorted) // 10**14, D // 10**14, 100)  # 根据xp和D值设定退出迭代的精度
    for _x in x_sorted:        # x在除数中，先进行小值的运算
        y = y * D // (_x * N)  # Small _x first
        S_i += _x
    # 这里 K0 中的prod(x) 不包含y的xp, 因为y值会迭代改变，所以不能加入for循环中
    # 需要在每次迭代时乘进去，变成完整的 prod
    for _x in x_sorted[::-1]:  # x在被除数中，先进行大值的运算
        K0_i = K0_i * _x * N // D  # Large _x first

    for j in range(255):
        y_prev = y

        K0 = K0_i * y * N // D  # 注意K0_i需要补上 y 的xp，变成完整的prod
        S = S_i + y             # 求和同理需要补上 y 的xp

        _g1k0 = abs(gamma + 10**18 - K0)

        # D / (A * N**N) * _g1k0**2 / gamma**2
        mul1 = 10**18 * D // gamma * _g1k0 // gamma * _g1k0 * A_MULTIPLIER // A

        # 2*K0 / _g1k0
        mul2 = 10**18 + (2 * 10**18) * K0 // _g1k0

        yfprime = (10**18 * y + S * mul2 + mul1 - D * mul2)
        fprime = yfprime // y
        assert fprime > 0  # Python only: f' > 0

        # y -= f / f_prime;  y = (y * fprime - f) / fprime
        y = (yfprime + 10**18 * D - 10**18 * S) // fprime + mul1 // fprime * (10**18 - K0) // K0

        if j > 100:  # Just logging when doesn't converge
            print(j, y, D, x)
        if y < 0 or fprime < 0:
            y = y_prev // 2
        if abs(y - y_prev) <= max(convergence_limit, y // 10**14):
            return y

    raise Exception("Did not converge")

4. 牛顿法的适用性和代码思路总结

4.1 牛顿法在 Defi 的适用性

牛顿法是一个万金油算法。在能给出较好的初值情况下，能够在 10 次以内解决大部分没有解析解的方程求值问题。因此适合用于绝大部分较为复杂的 Defi 数值算法，我们也相该算法会越来越普及被人进行使用。

普及牛顿法同时也为 Curve V1&V2 进行科普，这也是我们研究的初衷。在以上文章中我们看到了相较于教科书中的牛顿法，实际业务中的牛顿法使用起来具有较高的门槛。

4.2 牛顿法在 vyper&solidity 应用总结

决定对谁化简提出来作为公因子和，让谁成为优循环先生成的中间变量： 牛顿法在代码实现中有些中间变量是经过循环 N 次生成的。这些变量往往要结合数学化简时出现较多的变量形式进行统筹考虑。例如我们在 newton_D 函数中,发现 K0 及 K 具有较高的出现率，那么在设计中间变量是应该优先考虑的是 K0 或者 K 而不是 $K0$ 含有的 $n^n$ 或者 $d^n$ .
先乘后除原则 尽量减少分子/分母中的除法，将除法运算通分到分子分母中，使之变成乘法运算。乘法注意 EVM 数值溢出（如果产生数值溢出可以考虑咨询我们）。
求导会带来部分公式精度下降 需要手动去改变代码的精度来满足精度一致的前提。精度一致才能得到和数学公式中一样的结果。
适当的用简单的符号替代高频率出现的形式。
防止数值溢出和先大后小原则 在 EVM 执行牛顿法需要先对要执行连乘循环的数据要匹配合适的除法控制精度平衡以避免数值溢出。同时注意先执行大数的除法后执行小数的除法，也就是需要先讲数据按照从大到小的方式进行数据重排。

4.3 Curve V2 的代码理解难点

Curve V2 相较于 Uniswap V3 项目的理解起来最大的难点是：

Curve 更加偏数学优化，很多 Defi 代码逻辑是币圈原创。
Curve V2 95%以上的代码由 Curve CEO Michael 一人贡献，注释很少，其他人的给的注释有误
白皮书中有些关键地方 Michael 表述有误，导致理解困难
Curve 和 Uniswap 相比缺少他人研究的参考资料

4.4 Curve 其他算法及精度控制问题

本文由于篇幅所限，目前并未特别完整的将 Curve 中使用的牛顿法特别完整的表述出来。在实际业务代码中构建牛顿法另外一个难点是精度控制问题。精度控制问题完全值得另外一篇详细的文章来总结。

同时 Curve V2 的 math 库中还有其他的缺少注释的算法较难理解。比如 halfpow 函数实际是二项式算法在非整数领域的应用。

我们已经完整的理解了 Curve V1&V2 中的数学算法和具体代码。同时也较为完整的理解了 Curve V1&V2 的业务代码。

目前 0xstan 已经完成了 Curve V1 的核心合约进行 solidity 重构。

目前对 Curve V1 和 Curve V2 的 code review 部分已经放到 0xreviews.xyz 官网及 0xmc.com 上。