skip to content

Curve v1 StableSwap code review

By 0xstan & 0xmc

curve v1 通过实现 StableSwap 恒等式的交易池，达到比恒定乘积(Uniswap)交易池更高效低滑点的效果。适合相互之间价格稳定的交易对，比如两个稳定币(DAI-USDC)或同一锚定标的的资产(ETH-sETH synthetic ETH)。

overview

curve v1 核心公式

将恒定和等式与恒定乘积等式合并，给予系数 χ\chi (希腊字母)

χDn−1∑xi+∏xi=χDn+(Dn)n\chi D^{n-1}\sum x_i+\prod x_i=\chi D^n + (\frac{D}{n})^n

令 χ\chi 为如下表达

χ=A∏xi(D/n)n\chi=\frac{A\prod x_i}{(D/n)^n}

代入可得最终的核心公式

Ann∑xi+D=ADnn+Dn+1nn∏xiAn^n\sum x_i + D = ADn^n + \frac{D^{n+1}}{n^n\prod x_i}

pool-templates

pool 交易池合约有 5 种，他们基本构造方法相同，但有不同风格。(5 种合约模板参见 /contracts/pool-templates)

  • a: 用于交易 a-Token 类型的合约（余额自增的 token）的交易池子 aToken.balanceOf()
  • base: 基础的交易池子
  • eth: 带 ETH 的交易池子
  • meta: 元池，基本资产与 curve LP token 的交易池子
  • y: 用于交易 yearn-Token 类型的合约（可内生息的 token）的交易池子

使用模板合约部署交易池合约，主要修改以下初始化参数

  • ___USE_LENDING___: 布尔值数组，交易资产中是否有从借贷协议中借出的资产
  • ___N_COINS___: 池子中的资产种类数量
  • ___PRECISION_MUL___: 整型数组，每个资产的精度调整到 1e18 所需的乘数
  • ___RATES___: 整型数组，每个资产统一精度到 1e36 所需的乘数

Metapools 元池因为是某个资产和 base pool 类型的 lp token 组成交易对，所以还用了以下参数：

  • __BASE_N_COINS__: base pool 内的 N
  • __BASE_PRECISION_MUL__: base pool 内的 precision
  • __BASE_RATES__: base pool 内的 rates

pooldata.json 是主要用于测试的辅助参数，与合约内保持一致

{
    "wrapped_contract": "yERC20",   // 测试用的 wrapped token 合约
    "base_pool_contract": ""        // 元池中所对应的 base pool
    "coins": [                      // each list item represents 1 swappable coin within the pool
        {
            "decimals": 18,          // number of decimal places for the underlying coin
            "tethered": false,       // 调用token的 transfer/approve 操作是否返回 `None` (true 是没有返回，标准ERC20 应该有返回布尔值，但usdt没有返回值)
            "wrapped": true,         // token 是否为 wrapped token
            "wrapped_decimals": 18,  // wrapped token 的精度，如果不是wrapped可以省略
        },
    ]
    "rate_calculator_address": ""    // 计算兑换率的策略合约地址
}

base pool

基础的交易池子合约，例如 3pool

constans

合约中的常量

  • RATES 是一组汇率乘数，和 balances 相乘后，将精度统一到 1e36，最后和 PRECISION 相除，结果将统一成 1e18 精度
    • 在 base pool 中， RATES 将只起到统一精度的作用，但在特殊的池子中 (例如 y pool) RATES 不但要统一精度，还需要从外部合约获取 coin 和其底层资产之间的汇率
    • 详细情况参加后面对 y-pool 的解析
  • fee 以 1e10 为 100%
  • 手续费率，A 系数等参数可以经过治理投票后修改
  • A 系数的数值的修改是线性变化的
# These constants must be set prior to compiling
# 部署时的初始化参数
N_COINS: constant(int128) = ___N_COINS___
PRECISION_MUL: constant(uint256[N_COINS]) = ___PRECISION_MUL___
RATES: constant(uint256[N_COINS]) = ___RATES___

# fixed constants
FEE_DENOMINATOR: constant(uint256) = 10 ** 10 # 计算手续费时的分母
PRECISION: constant(uint256) = 10 ** 18  # 计算资产数量时需要统一到的精度水平

MAX_ADMIN_FEE: constant(uint256) = 10 * 10 ** 9 # 管理员手续费率的最大值，设置费率不能超过此值 10%
MAX_FEE: constant(uint256) = 5 * 10 ** 9 # 手续费率的最大值，设置费率不能超过此值 5%
MAX_A: constant(uint256) = 10 ** 6 # A 系数的最大值，当前3pool A = 2000
MAX_A_CHANGE: constant(uint256) = 10 # 规定每次对A的调整不能超过原有值的倍数范围 即 1/10 * A <= A' <= 10*A

ADMIN_ACTIONS_DELAY: constant(uint256) = 3 * 86400 # 配置更改的延迟生效时间
MIN_RAMP_TIME: constant(uint256) = 86400 # 线性修改A系数的最小时间间隔

A_PRECISION: constant(uint256) = 100 # A 的计算精度
KILL_DEADLINE_DT: constant(uint256) = 2 * 30 * 86400 # 部署合约多久后才能调用 kill_me 方法

variables

  • 注意 A 的值是 A*N_COINS**(N_COINS-1), 因为涉及 A 的计算部分都有 N**(N-1)，所以直接将乘积作为 A 值
coins: public(address[N_COINS]) # 资产 token 地址数组
balances: public(uint256[N_COINS]) # 资产的数量
fee: public(uint256)  # fee * 1e10
admin_fee: public(uint256)  # admin_fee * 1e10

owner: public(address)
lp_token: public(address)

initial_A: public(uint256) # A 的初始值，或调整之前的值
future_A: public(uint256) # A 的当前值，或调整的目标值
initial_A_time: public(uint256) # A 的调整开始时间
future_A_time: public(uint256) # A 的调整完成时间

admin_actions_deadline: public(uint256) # 当调整commit提交后，管理员执行调整的 deadline
transfer_ownership_deadline: public(uint256) # 当移交所有权commit提交后，管理员执行调整的 deadline
future_fee: public(uint256) # 调整手续费率的目标值
future_admin_fee: public(uint256) # 调整管理员手续费率的目标值
future_owner: public(address) # 调整所有权的目标地址

is_killed: bool
kill_deadline: uint256

functions

constructor

@external
def __init__(
    _owner: address,
    _coins: address[N_COINS],
    _pool_token: address,
    _A: uint256,
    _fee: uint256,
    _admin_fee: uint256
):
    """
    @notice Contract constructor
    @param _owner Contract owner address
    @param _coins Addresses of ERC20 conracts of coins
    @param _pool_token Address of the token representing LP share
    @param _A Amplification coefficient multiplied by n * (n - 1)
    @param _fee Fee to charge for exchanges
    @param _admin_fee Admin fee
    """
    for i in range(N_COINS):
        assert _coins[i] != ZERO_ADDRESS
    self.coins = _coins
    self.initial_A = _A * A_PRECISION
    self.future_A = _A * A_PRECISION
    self.fee = _fee
    self.admin_fee = _admin_fee
    self.owner = _owner
    self.kill_deadline = block.timestamp + KILL_DEADLINE_DT
    self.lp_token = _pool_token

A

主要逻辑在 _A()，由于 A 系数不能突然发生较大变化，这样造成的内部价格突然变化，从而导致被外部套利者利用，套走过多资产。所以对 A 修改是线性变化的，而非立即变成目标值。其计算逻辑可改写为如下形式：

A_current = A_initial + abs(A_future - A_initial) * (t_current - t_initial) / (t_future - t_initial)

观察核心公式可知，A 值越大，恒定和等式部分的项权重越大，其图形就越趋近于直线，A 值越小则趋近于恒定乘积的等式，图形更为弯曲（当 N=2 时，可以理解为更趋近于 Uniswap 的形状）。所以当 A 值变化时，图形的弯曲程度会发生改变，资产之间的价格也随之改变。如果突然有很大的变化，会导致池子内部价格与外部价格偏差过大，产生较大的套利空间。

@view
@internal
def _A() -> uint256:
    """
    Handle ramping A up or down
    """
    t1: uint256 = self.future_A_time
    A1: uint256 = self.future_A

    if block.timestamp < t1:
        A0: uint256 = self.initial_A
        t0: uint256 = self.initial_A_time
        # Expressions in uint256 cannot have negative numbers, thus "if"
        # 因为合约中不能有负值，所以这里要判断大小，给出减法的顺序
        if A1 > A0:
            return A0 + (A1 - A0) * (block.timestamp - t0) / (t1 - t0)
        else:
            return A0 - (A0 - A1) * (block.timestamp - t0) / (t1 - t0)

    else:  # when t1 == 0 or block.timestamp >= t1
        return A1


@view
@external
def A() -> uint256:
    return self._A() / A_PRECISION


@view
@external
def A_precise() -> uint256:
    return self._A()

xp

存放每个资产价值(balance * price)的数组

  • base-pool 中，RATES是统一精度的数组，但其实是因为资产是锚定同一种标的的token，比如稳定币之间，都锚定美元，所以price都是1
  • 而在 a-pool 和 y-pool 中，RATES 将包含价格 详见 a-pool, y-pool
'''返回当前池子的xp'''
@view
@internal
def _xp() -> uint256[N_COINS]:
    result: uint256[N_COINS] = RATES
    for i in range(N_COINS):
        result[i] = result[i] * self.balances[i] / PRECISION
    return result


'''指定balance数量计算xp'''
@pure
@internal
def _xp_mem(_balances: uint256[N_COINS]) -> uint256[N_COINS]:
    result: uint256[N_COINS] = RATES
    for i in range(N_COINS):
        result[i] = result[i] * _balances[i] / PRECISION
    return result

virtual_price

virtual_price = D / lp_totalSupply

  • D 的单位与 DAI 相似，精度 1e18
  • 当价格处于平衡点，D = n * 每个资产的总价值
  • 此时 D 就是整个池子资产组合的总(虚拟)价值
@view
@external
def get_virtual_price() -> uint256:
    """
    @notice The current virtual price of the pool LP token
    @dev Useful for calculating profits
    @return LP token virtual price normalized to 1e18
    """
    D: uint256 = self._get_D(self._xp(), self._A())
    # D is in the units similar to DAI (e.g. converted to precision 1e18)
    # When balanced, D = n * x_u - total virtual value of the portfolio
    token_supply: uint256 = ERC20(self.lp_token).totalSupply()
    return D * PRECISION / token_supply

calc_token_amount

计算调用 deposit 和 withdraw 后，lp token 的变化数量。该方法会考虑滑点的影响，但不包括手续费。主要用于防止抢跑攻击，而非用于交易的精确计算。

根据 D 的变化比例来同比计算 lp token 的变化。

@view
@external
def calc_token_amount(_amounts: uint256[N_COINS], _is_deposit: bool) -> uint256:
    """
    @notice Calculate addition or reduction in token supply from a deposit or withdrawal
    @dev This calculation accounts for slippage, but not fees.
         Needed to prevent front-running, not for precise calculations!
    @param _amounts Amount of each coin being deposited
    @param _is_deposit set True for deposits, False for withdrawals
    @return Expected amount of LP tokens received
    """
    amp: uint256 = self._A()
    balances: uint256[N_COINS] = self.balances
    D0: uint256 = self._get_D_mem(balances, amp) # 缓存变化之前的D
    for i in range(N_COINS): # 遍历改变每个资产的数量
        if _is_deposit:
            balances[i] += _amounts[i]
        else:
            balances[i] -= _amounts[i]
    D1: uint256 = self._get_D_mem(balances, amp) # 计算变化之后的D
    token_amount: uint256 = CurveToken(self.lp_token).totalSupply()
    diff: uint256 = 0
    if _is_deposit:
        diff = D1 - D0
    else:
        diff = D0 - D1
    # 根据D的变化比例计算lp token变化量
    # (delta D / D0) * totalSupply
    return diff * token_amount / D0

add_liquidity

添加流动性，向池子注入资产。传入资产数量数组和最小 lp token mint 数量，返回实际 mint 的数量。

  1. 根据传入 token 数量，计算 D 的增量 delta D1
    • 不考虑手续费的影响
    • assert delta D1 > 0
  2. 考虑手续费的影响，计算 D 的增量 delta D2
    • 先算出不考虑手续费时，每个资产的变化数量(difference_balance)
    • 根据费率分别计算每个资产的手续费
    • fee_i = fee_rate * difference_balance
    • 将资产数量减去手续费的数量，然后重新计算考虑手续费影响的 D 值，进而得到 delta D2
  3. 根据 delta D2 与 D 的比例，同比计算新增 lp token 数量
    • mint amount = (delta D2 / D) * totalSupply
    • 如果 mint 数量 < 设定的最小数量，交易回滚
  4. 将资产 token 从用户转入本合约，为用户 mint lp token，最后返回实际 mint 数量

关于 lp token 流动性数量的含义：

  • 池子首次添加流动性，不会收取手续费，且 mint 数量就是 D 值
  • 如果不考虑手续费影响，lp token 数量与 D 值同步
  • 如果添加流动性的资产比例，不会改变当前价格，其过程也不会发生交易，因此就不会产生手续费

admin_fee 是一个百分比，当前是 50%，含义是协议将手续手续中的一定比例，作为协议费用。收取的协议费(admin fee) 的资产不会计入 balances 字段，所以 ERC20.balanceOf(this) - self.balance 将是现阶段可收取的 admin_fee。

关于 N_COINS / (4 * (N_COINS - 1))

  • 不平衡的添加流动性时，会针对不平衡的部分收取交易手续费，但因为用户只存入了输入 token，并没有提出输出 token，该交易并不完整，所以需要让手续费乘以一个减小系数
  • 当 N = 2 时，该系数将是最高的 1/2
  • 当 N 非常大，该系数将无限趋近于 1/4
@external
@nonreentrant('lock')
def add_liquidity(_amounts: uint256[N_COINS], _min_mint_amount: uint256) -> uint256:
    """
    @notice Deposit coins into the pool
    @param _amounts List of amounts of coins to deposit
    @param _min_mint_amount Minimum amount of LP tokens to mint from the deposit
    @return Amount of LP tokens received by depositing
    """
    assert not self.is_killed  # dev: is killed

    amp: uint256 = self._A()
    old_balances: uint256[N_COINS] = self.balances

    # Initial invariant
    # 计算变化前的D数值
    D0: uint256 = self._get_D_mem(old_balances, amp)

    lp_token: address = self.lp_token
    token_supply: uint256 = CurveToken(lp_token).totalSupply()
    new_balances: uint256[N_COINS] = old_balances
    for i in range(N_COINS):
        if token_supply == 0:
            assert _amounts[i] > 0  # 初次添加流动性，每种资产的数量都必须大于0
        # balances store amounts of c-tokens
        # ?? 这里注释有疑问，base pool 应该不会有c-token ??
        new_balances[i] += _amounts[i]

    # Invariant after change
    # 计算变化后的D值（不考虑手续费影响）
    D1: uint256 = self._get_D_mem(new_balances, amp)
    assert D1 > D0

    # We need to recalculate the invariant accounting for fees
    # to calculate fair user's share
    # 我们需要公平的计算用户的份额（考虑手续费）
    D2: uint256 = D1
    fees: uint256[N_COINS] = empty(uint256[N_COINS])
    mint_amount: uint256 = 0
    if token_supply > 0:
        # Only account for fees if we are not the first to deposit
        # 初次添加流动性不会收取手续费，换言之，后续的添加都会收取
        # N_COINS / (4 * (N_COINS - 1)) 的意义是可以根据N来调节手续费
        # 当 N = 2 时，该系数将是最高的 1/2
        # 当 N 非常大，该系数将无限趋近于 1/4
        fee: uint256 = self.fee * N_COINS / (4 * (N_COINS - 1))
        admin_fee: uint256 = self.admin_fee
        for i in range(N_COINS):
            # ideal_balance 每个资产理想的数量不考虑手续费
            # difference 每个资产理想数值与现值的差量
            # fee_i = difference * fee_rate
            # 实际资产数量 = 理想数量 - 手续费
            # new_balance_i = ideal_balance - fee_i
            ideal_balance: uint256 = D1 * old_balances[i] / D0
            difference: uint256 = 0
            new_balance: uint256 = new_balances[i]
            if ideal_balance > new_balance:
                difference = ideal_balance - new_balance
            else:
                difference = new_balance - ideal_balance
            fees[i] = fee * difference / FEE_DENOMINATOR
            self.balances[i] = new_balance - (fees[i] * admin_fee / FEE_DENOMINATOR)
            new_balances[i] -= fees[i]
        # 根据扣除手续费之后的资产数量，计算新的D值
        # 然后同比计算 lp token 的增量，即为 mint 数量
        D2 = self._get_D_mem(new_balances, amp)
        mint_amount = token_supply * (D2 - D0) / D0
    else:
        # 初次添加流动性，不收取手续费，池子资产数量即为本地添加的数量
        # lp token 数量就是D，
        self.balances = new_balances
        mint_amount = D1  # Take the dust if there was any
    assert mint_amount >= _min_mint_amount, "Slippage screwed you"

    # Take coins from the sender
    for i in range(N_COINS):
        if _amounts[i] > 0:
            # "safeTransferFrom" which works for ERC20s which return bool or not
            _response: Bytes[32] = raw_call(
                self.coins[i],
                concat(
                    method_id("transferFrom(address,address,uint256)"),
                    convert(msg.sender, bytes32),
                    convert(self, bytes32),
                    convert(_amounts[i], bytes32),
                ),
                max_outsize=32,
            )
            if len(_response) > 0:
                assert convert(_response, bool)  # dev: failed transfer
            # end "safeTransferFrom"

    # Mint pool tokens
    CurveToken(lp_token).mint(msg.sender, mint_amount)

    log AddLiquidity(msg.sender, _amounts, fees, D1, token_supply + mint_amount)

    return mint_amount

exchange

交易，输入单一资产 i，输出另一个单一资产 j，规定最小获得的输出数量 _min_dy，返回实际交易输出数量 (dy)。

@external
@nonreentrant('lock')
def exchange(i: int128, j: int128, _dx: uint256, _min_dy: uint256) -> uint256:
    """
    @notice Perform an exchange between two coins
    @dev Index values can be found via the `coins` public getter method
    @param i Index value for the coin to send
    @param j Index valie of the coin to recieve
    @param _dx Amount of `i` being exchanged
    @param _min_dy Minimum amount of `j` to receive
    @return Actual amount of `j` received
    """
    assert not self.is_killed  # dev: is killed

    # 根据当前资产数量计算现有每个资产的总价值 xp
    old_balances: uint256[N_COINS] = self.balances
    xp: uint256[N_COINS] = self._xp_mem(old_balances)

    # 计算输入资产后，输出资产的价值，即y
    rates: uint256[N_COINS] = RATES
    x: uint256 = xp[i] + _dx * rates[i] / PRECISION
    y: uint256 = self._get_y(i, j, x, xp)

    # 计算输出资产的价值变化量，即 dy
    # 防止计算精度引起的数值不准确，向下舍入 (-1)
    # 计算手续费价值 dy_fee
    dy: uint256 = xp[j] - y - 1  # -1 just in case there were some rounding errors
    dy_fee: uint256 = dy * self.fee / FEE_DENOMINATOR

    # Convert all to real units
    # 将扣除手续费后的价值 (dy - dy_fee) , 并统一精度 PRECISION = 1e18
    dy = (dy - dy_fee) * PRECISION / rates[j]
    assert dy >= _min_dy, "Exchange resulted in fewer coins than expected"

    # 从手续费价值中抽取一定比例的协议费，并转根据价格转换成实际的输出资产数量
    dy_admin_fee: uint256 = dy_fee * self.admin_fee / FEE_DENOMINATOR
    dy_admin_fee = dy_admin_fee * PRECISION / rates[j]

    # Change balances exactly in same way as we change actual ERC20 coin amounts
    # 将输入数量加到balances上，我们实际运算的是 ERC20 数量
    self.balances[i] = old_balances[i] + _dx
    # When rounding errors happen, we undercharge admin fee in favor of LP
    # 当舍入错误发生，协议将不收取协议费来支持流动性的发展
    # 除以 FEE_DENOMINATOR 时，会将小于 FEE_DENOMINATOR 的数量舍入，所以认为这部分是少收了协议费
    #
    # 输出资产的数量 减去实际输出给用户的数量(fee会保留在合约中)， 再扣除协议费数量
    # 值得注意的是，这里 balance - dy 已经将交易手续费fee留给了 lp 提供者
    # 然后协议又从 lp 提供者的fee份额中，抽取了协议费
    self.balances[j] = old_balances[j] - dy - dy_admin_fee

    # 转入输入资产
    _response: Bytes[32] = raw_call(
        self.coins[i],
        concat(
            method_id("transferFrom(address,address,uint256)"),
            convert(msg.sender, bytes32),
            convert(self, bytes32),
            convert(_dx, bytes32),
        ),
        max_outsize=32,
    )
    if len(_response) > 0:
        assert convert(_response, bool)

    # 转出输出资产
    _response = raw_call(
        self.coins[j],
        concat(
            method_id("transfer(address,uint256)"),
            convert(msg.sender, bytes32),
            convert(dy, bytes32),
        ),
        max_outsize=32,
    )
    if len(_response) > 0:
        assert convert(_response, bool)

    log TokenExchange(msg.sender, i, _dx, j, dy)

    return dy

remove_liquidity

移除流动性，传入要移除的 lp token 数量 _amount ，最小赎回资产数量数组 _min_amounts，转给调用者的资产数量将按照池子当前的资产比分配，返回赎回的资产数量数组。

由于该方法将保持池子内现有的资产比例，不会引起价格改变，该方法不收取手续费。

@external
@nonreentrant('lock')
def remove_liquidity(_amount: uint256, _min_amounts: uint256[N_COINS]) -> uint256[N_COINS]:
    """
    @notice Withdraw coins from the pool
    @dev Withdrawal amounts are based on current deposit ratios
    @param _amount Quantity of LP tokens to burn in the withdrawal
    @param _min_amounts Minimum amounts of underlying coins to receive
    @return List of amounts of coins that were withdrawn
    """
    lp_token: address = self.lp_token
    total_supply: uint256 = CurveToken(lp_token).totalSupply()
    amounts: uint256[N_COINS] = empty(uint256[N_COINS])

    for i in range(N_COINS):
        # 根据移除的 lp token 数量与总数的比例，同比计算balance的变化量，即为赎回的数量
        # 这里没有收取手续费
        old_balance: uint256 = self.balances[i]
        value: uint256 = old_balance * _amount / total_supply
        assert value >= _min_amounts[i], "Withdrawal resulted in fewer coins than expected"
        self.balances[i] = old_balance - value
        amounts[i] = value
        _response: Bytes[32] = raw_call(
            self.coins[i],
            concat(
                method_id("transfer(address,uint256)"),
                convert(msg.sender, bytes32),
                convert(value, bytes32),
            ),
            max_outsize=32,
        )
        if len(_response) > 0:
            assert convert(_response, bool)

    CurveToken(lp_token).burnFrom(msg.sender, _amount)  # dev: insufficient funds

    log RemoveLiquidity(msg.sender, amounts, empty(uint256[N_COINS]), total_supply - _amount)

    return amounts

remove_liquidity_imbalance

(不平衡的)移除流动性，传入要赎回的资产数量数组 _amounts, 最大能销毁的 lp token 数量 _max_burn_amount，转给调用者的资产数量将按照入参分配，返回实际销毁掉的 lp token 数量。

由于其中包含引起不平衡的流动性，导致池子内资产数量比例发生变化，进而导致价格改变，该方法要收取手续费。

  1. 根据传入 token 数量，计算 D 的减量 delta D1
    • 不考虑手续费的影响
  2. 考虑手续费的影响，计算 D 的减量 delta D2
    • 先算出不考虑手续费时，流动性中引起资产不平衡的数量(difference_balance)
    • 根据费率分别计算每个资产的手续费
    • fee_i = fee_rate * difference_balance
    • 将资产数量减去手续费的数量，然后重新计算考虑手续费影响的 D 值，进而得到 delta D2
    • 由于余额部分已经扣除了手续费，所以根据 new_balance 计算 D 值会略少于真实的 D 值，这部分将导致销毁更多的 LP token
    • 即，该函数将保证用户赎回资产的数量和 _amounts 保持一致，但会多销毁 LP token，作为手续费
  3. 根据 delta D2 与 D 的比例，同比计算减少 lp token 数量
    • burn_amount = (delta D2 / D) * totalSupply
    • assert burn_amount != 0
    • assert burn_amount <= _max_burn_amount
  4. 将资产按照入参的数量转给用户，销毁用户的 lp token，最后返回实际 burn 数量
@external
@nonreentrant('lock')
def remove_liquidity_imbalance(_amounts: uint256[N_COINS], _max_burn_amount: uint256) -> uint256:
    """
    @notice Withdraw coins from the pool in an imbalanced amount
    @param _amounts List of amounts of underlying coins to withdraw
    @param _max_burn_amount Maximum amount of LP token to burn in the withdrawal
    @return Actual amount of the LP token burned in the withdrawal
    """
    assert not self.is_killed  # dev: is killed

    # 计算变化前的D值
    amp: uint256 = self._A()
    old_balances: uint256[N_COINS] = self.balances
    D0: uint256 = self._get_D_mem(old_balances, amp)
    new_balances: uint256[N_COINS] = old_balances
    for i in range(N_COINS):
        new_balances[i] -= _amounts[i]
    # 计算移除指定资产数量后的 D 值
    D1: uint256 = self._get_D_mem(new_balances, amp)

    # N_COINS / (4 * (N_COINS - 1)) 的含义参照前文描述
    fee: uint256 = self.fee * N_COINS / (4 * (N_COINS - 1))
    admin_fee: uint256 = self.admin_fee
    fees: uint256[N_COINS] = empty(uint256[N_COINS])
    for i in range(N_COINS):
        new_balance: uint256 = new_balances[i]
        ideal_balance: uint256 = D1 * old_balances[i] / D0
        difference: uint256 = 0
        if ideal_balance > new_balance:
            difference = ideal_balance - new_balance
        else:
            difference = new_balance - ideal_balance
        fees[i] = fee * difference / FEE_DENOMINATOR
        # 全局balances只减去 admin_fee 部分
        # 而用于后续计算 D 值的 new_balances 将扣除完整的手续费
        self.balances[i] = new_balance - (fees[i] * admin_fee / FEE_DENOMINATOR)
        new_balances[i] = new_balance - fees[i]
    # D2 将比实际的 D 值略小，因为扣除了手续费的价值
    # 后续将导致多销毁调用者的 LP token
    D2: uint256 = self._get_D_mem(new_balances, amp)

    lp_token: address = self.lp_token
    token_supply: uint256 = CurveToken(lp_token).totalSupply()
    token_amount: uint256 = (D0 - D2) * token_supply / D0
    assert token_amount != 0  # dev: zero tokens burned
    token_amount += 1  # In case of rounding errors - make it unfavorable for the "attacker"
    assert token_amount <= _max_burn_amount, "Slippage screwed you"

    CurveToken(lp_token).burnFrom(msg.sender, token_amount)  # dev: insufficient funds
    for i in range(N_COINS):
        if _amounts[i] != 0:
            _response: Bytes[32] = raw_call(
                self.coins[i],
                concat(
                    method_id("transfer(address,uint256)"),
                    convert(msg.sender, bytes32),
                    convert(_amounts[i], bytes32),
                ),
                max_outsize=32,
            )
            if len(_response) > 0:
                assert convert(_response, bool)

    log RemoveLiquidityImbalance(msg.sender, _amounts, fees, D1, token_supply - token_amount)

    return token_amount

D

由于 curve 的平衡方程，无法直接写出 D 的解析式，curve 在合约中使用了牛顿法迭代求近似解。

xn+1=xn−f(xn)f′(xn)x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}

简单理解牛顿法就是利用上述公式，不断迭代 x_n+1 的值，使其越来越逼近真实的解

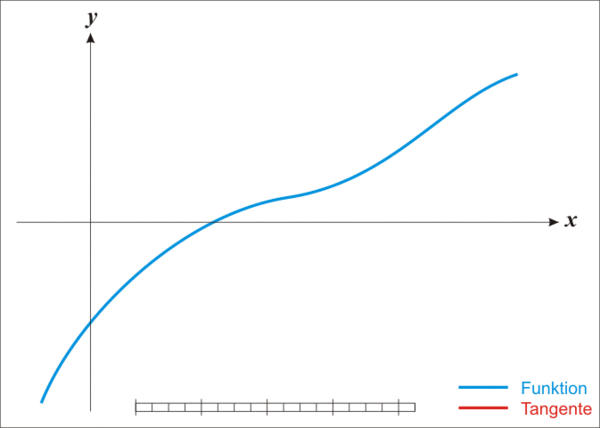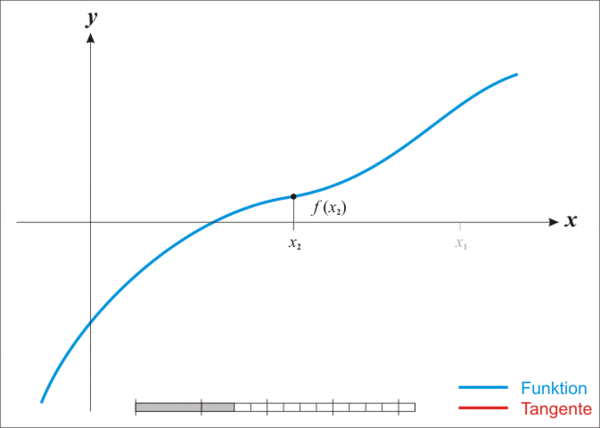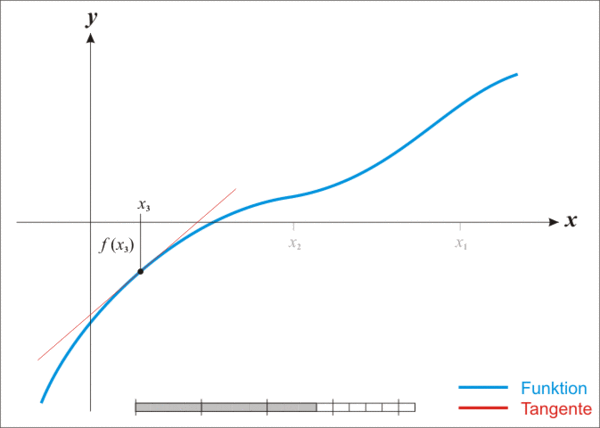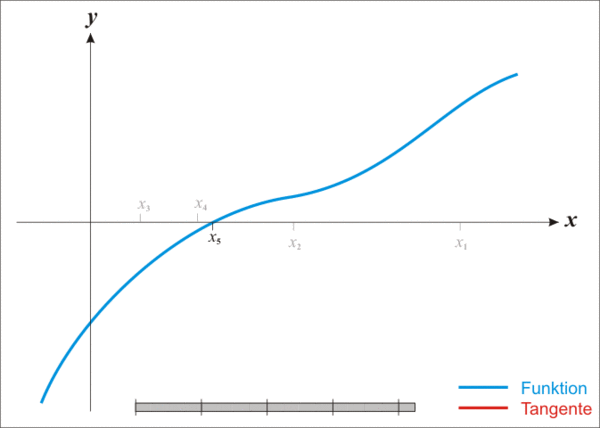
newton's method

代码中使用的牛顿法的函数 f(D)，是用核心公式推导得来，下面简述推导过程：

  1. 首先将核心公式变形成 f(D) = 0 的形式

    f(D)=Ann∑xi+D−ADnn−Dn+1nn∏xif(D)=An^n\sum x_i + D-ADn^n-\frac{D^{n+1}}{n^n\prod x_i}

  2. D_new = D - f(D)/f'(D)

    Dnew=D−Ann∑xi+D−ADnn−Dn+1nn∏xi1−Ann−(n+1)Dnnn∏xiD_{new}=D-\frac{An^n\sum x_i + D-ADn^n-\frac{D^{n+1}}{n^n\prod x_i}}{1-An^n-(n+1)\frac{D^n}{n^n\prod x_i}}

  3. 最终变成代码中的形态

    Dnew=Ann∑xi−Dn+1nn∏xiAnn+(n+1)Dnnn∏xi−1D_{new}=\frac{An^n\sum x_i-\frac{D^{n+1}}{n^n\prod x_i}}{An^n+(n+1)\frac{D^n}{n^n\prod x_i}-1}

  4. for 循环迭代求 D 的解，当迭代到 D 与上一次的差值 <= 1 时，停止迭代；

  5. 通常轮迭代不超过 4 轮就会找到最优解；但如果迭代 255 次仍然没有找到合适的解，程序终止，交易回滚 (revert)；用户可以通过 remove_liquidity 方法回收资产；

注意：注释中的牛顿法公式写漏了一项，而代码写的是正确的化简后的公式。

@pure
@internal
def _get_D(_xp: uint256[N_COINS], _amp: uint256) -> uint256:
    """
    D invariant calculation in non-overflowing integer operations
    iteratively

    A * sum(x_i) * n**n + D = A * D * n**n + D**(n+1) / (n**n * prod(x_i))

    Converging solution:
    D[j+1] = (A * n**n * sum(x_i) - D[j]**(n+1) / (n**n prod(x_i))) / (A * n**n + (n+1)*D[j]**n/(n**n prod(x_i)) - 1)

    这里原版代码注释分母漏掉了一项
    (n+1)*D[j]**n/(n**n prod(x_i))

    原版代码链接:
    https://github.com/curvefi/curve-contract/blob/master/contracts/pool-templates/base/SwapTemplateBase.vy#L214
    """
    S: uint256 = 0
    Dprev: uint256 = 0

    for _x in _xp:
        S += _x
    if S == 0:
        return 0

    D: uint256 = S
    Ann: uint256 = _amp * N_COINS
    for _i in range(255):
        D_P: uint256 = D
        for _x in _xp:
            D_P = D_P * D / (_x * N_COINS)  # If division by 0, this will be borked: only withdrawal will work. And that is good
            # 只有当移除流动性时才有可能 _x 为0，这时程序会崩溃
            # 只能平衡的移除流动性, remove_liquidity 不会调用牛顿法求解，这也是期望的结果
            # 添加流动性，池内的xp值不可能为0
        Dprev = D
        D = (Ann * S / A_PRECISION + D_P * N_COINS) * D / ((Ann - A_PRECISION) * D / A_PRECISION + (N_COINS + 1) * D_P)
        # Equality with the precision of 1
        # 当迭代的新值和上次之差，小于等于 1，即0或1
        # 认为找到了局部最优解
        if D > Dprev:
            if D - Dprev <= 1:
                return D
        else:
            if Dprev - D <= 1:
                return D
    # convergence typically occurs in 4 rounds or less, this should be unreachable!
    # if it does happen the pool is borked and LPs can withdraw via `remove_liquidity`
    raise


@view
@internal
def _get_D_mem(_balances: uint256[N_COINS], _amp: uint256) -> uint256:
    return self._get_D(self._xp_mem(_balances), _amp)

y

输入资产 i ，变化之后的数量 x，变化之前的 _xp，计算输出资产 j 变化后的数量。

与计算 D 一样，这里也使用了牛顿法计算 y, 即 x_j，其 f(x_j) 推导过程如下：

Ann∑xi+D=ADnn+Dn+1nn∏xiAn^n\sum x_i + D = ADn^n + \frac{D^{n+1}}{n^n\prod x_i}

  1. 设 sum', prod' 分别为排除输出资产数量的累加和累乘结果

    • sum' = sum(x) - x_j
    • prod' = prod(x) / x_j

  2. 核心公式除以 A*n**n

    ∑xi+DAnn−D=Dn+1Annnn∏xi\sum{x_i}+\frac{D}{An^n}-D=\frac{D^{n+1}}{An^nn^n\prod x_i}

  3. 乘以 x_j，并代入 sum' 和 prod'

    xj(xj+sum′)−xj(Ann−1)DAnn=Dn+1xjAn2n(prod′∗xj)x_j(x_j+sum')-x_j(An^n-1)\frac{D}{An^n}=\frac{D^{n+1}x_j}{An^{2n}(prod'*x_j)}

  4. 展开多项式，即为牛顿法使用的 f(x_j)

    xj2+xj(sum′−(Ann−1)DAnn)=Dn+1An2nprod′x_j^2+x_j(sum'-(An^n-1)\frac{D}{An^n})=\frac{D^{n+1}}{An^{2n}prod'}

  5. 将其写为 x_j**2 + b*x_j = c 形式，代入牛顿法公式 x = x - f(x) / f'(x)

    • x_j = (x_j**2 + c) / (2*x_j + b)
@view
@internal
def _get_y(i: int128, j: int128, x: uint256, _xp: uint256[N_COINS]) -> uint256:
    """
    Calculate x[j] if one makes x[i] = x

    Done by solving quadratic equation iteratively.
    x_1**2 + x_1 * (sum' - (A*n**n - 1) * D / (A * n**n)) = D ** (n + 1) / (n ** (2 * n) * prod' * A)
    x_1**2 + b*x_1 = c

    x_1 = (x_1**2 + c) / (2*x_1 + b)
    """
    # x in the input is converted to the same price/precision

    assert i != j       # dev: same coin
    assert j >= 0       # dev: j below zero
    assert j < N_COINS  # dev: j above N_COINS

    # should be unreachable, but good for safety
    assert i >= 0
    assert i < N_COINS

    A: uint256 = self._A()
    D: uint256 = self._get_D(_xp, A)
    Ann: uint256 = A * N_COINS
    c: uint256 = D      # c 提前乘以D
    S: uint256 = 0
    _x: uint256 = 0
    y_prev: uint256 = 0

    # for 排除 i == j 的情况，即排除输出资产的xp
    # c将被乘以 N-1 次 D
    for _i in range(N_COINS):
        if _i == i:
            _x = x
        elif _i != j:
            _x = _xp[_i]
        else:
            continue
        S += _x
        c = c * D / (_x * N_COINS)
    # for循环之后，c中含有 D^N ，而根据公式，还需要乘以一次 D
    c = c * D * A_PRECISION / (Ann * N_COINS)
    b: uint256 = S + D * A_PRECISION / Ann  # - D
    y: uint256 = D      # 牛顿法的初值设为 D
    for _i in range(255):
        y_prev = y
        y = (y*y + c) / (2 * y + b - D)
        # Equality with the precision of 1
        if y > y_prev:
            if y - y_prev <= 1:
                return y
        else:
            if y_prev - y <= 1:
                return y
    raise


@view
@external
def get_dy(i: int128, j: int128, _dx: uint256) -> uint256:
    xp: uint256[N_COINS] = self._xp()
    rates: uint256[N_COINS] = RATES

    x: uint256 = xp[i] + (_dx * rates[i] / PRECISION)
    y: uint256 = self._get_y(i, j, x, xp)
    dy: uint256 = xp[j] - y - 1
    fee: uint256 = self.fee * dy / FEE_DENOMINATOR
    return (dy - fee) * PRECISION / rates[j]

还有个 _get_y_D() 函数，与上述区别是可以自定义 D 的值来求 y

@pure
@internal
def _get_y_D(A: uint256, i: int128, _xp: uint256[N_COINS], D: uint256) -> uint256:

calc_withdraw_one_coin

指定移除流动性 LP token 的数量，计算只赎回单一资产的数量。

  1. 根据 _token_amount 和 total_supply 的比例，同比计算不考虑手续费的 D 值
  2. 根据新的 D 值计算此次移除，产生的交易量，收取手续费
  3. 根据扣除手续费新的数量，计算实际的 D 值
@view
@internal
def _calc_withdraw_one_coin(_token_amount: uint256, i: int128) -> (uint256, uint256, uint256):
    # First, need to calculate
    # * Get current D
    # * Solve Eqn against y_i for D - _token_amount
    # 首先需要先计算出移除流动性后，资产i的新数量
    amp: uint256 = self._A()
    xp: uint256[N_COINS] = self._xp()
    D0: uint256 = self._get_D(xp, amp)

    # 根据 lp token 变化量同比计算D的新值
    # 牛顿法计算新的资产 i 的数量 new_y - 不考虑手续费
    # xp_reduced 资产价值减少后的量
    total_supply: uint256 = CurveToken(self.lp_token).totalSupply()
    D1: uint256 = D0 - _token_amount * D0 / total_supply
    new_y: uint256 = self._get_y_D(amp, i, xp, D1)
    xp_reduced: uint256[N_COINS] = xp
    fee: uint256 = self.fee * N_COINS / (4 * (N_COINS - 1))
    for j in range(N_COINS):
        # dx_expected 资产j价值的变量
        #   - 相对于按照比例移除流动性的数量
        #   - 不考虑手续费
        # 资产i相对新的xp要少，其他则是相对于新的xp要多，因此需要注意正负号
        dx_expected: uint256 = 0
        if j == i:
            dx_expected = xp[j] * D1 / D0 - new_y
        else:
            dx_expected = xp[j] - xp[j] * D1 / D0
        # 在输出资产上扣除手续费
        xp_reduced[j] -= fee * dx_expected / FEE_DENOMINATOR

    # 使用扣除手续费的xp计算 y，进而得出dy
    dy: uint256 = xp_reduced[i] - self.get_y_D(amp, i, xp_reduced, D1)
    precisions: uint256[N_COINS] = PRECISION_MUL
    dy = (dy - 1) / precisions[i]  # Withdraw less to account for rounding errors
    dy_0: uint256 = (xp[i] - new_y) / precisions[i]  # w/o fees

    # 返回 赎回的资产数量，扣除的手续费(价值), lp token 总量（销毁之前）
    return dy, dy_0 - dy, total_supply


@view
@external
def calc_withdraw_one_coin(_token_amount: uint256, i: int128) -> uint256:
    """
    @notice Calculate the amount received when withdrawing a single coin
    @param _token_amount Amount of LP tokens to burn in the withdrawal
    @param i Index value of the coin to withdraw
    @return Amount of coin received
    """
    return self._calc_withdraw_one_coin(_token_amount, i)[0]

remove_liquidity_one_coin

移除流动性，赎回单一种类资产。可以认为这期间是将其他资产交易为了单一资产，需要手续手续费。

传入要销毁的 lp token 数量 _token_amount，赎回资产序号 i, 最小要收到的资产数量 _min_amount， 返回实际赎回的资产数量。

@external
@nonreentrant('lock')
def remove_liquidity_one_coin(_token_amount: uint256, i: int128, _min_amount: uint256) -> uint256:
    """
    @notice Withdraw a single coin from the pool
    @param _token_amount Amount of LP tokens to burn in the withdrawal
    @param i Index value of the coin to withdraw
    @param _min_amount Minimum amount of coin to receive
    @return Amount of coin received
    """
    assert not self.is_killed  # dev: is killed

    # 预先计算本次移除将赎回的资产数量 dy
    # 如果 dy 小于设定的最小数量，交易回滚
    dy: uint256 = 0
    dy_fee: uint256 = 0
    total_supply: uint256 = 0
    dy, dy_fee, total_supply = self._calc_withdraw_one_coin(_token_amount, i)
    assert dy >= _min_amount, "Not enough coins removed"

    # 将 admin fee 从balances中扣除
    # 销毁掉设定的 lp token 数量
    #
    # 注意 _calc_withdraw_one_coin() 返回的 dy 是已经扣除掉手续费的数量
    # 所以这里需要单独从balances中扣除协议费
    self.balances[i] -= (dy + dy_fee * self.admin_fee / FEE_DENOMINATOR)
    CurveToken(self.lp_token).burnFrom(msg.sender, _token_amount)  # dev: insufficient funds

    # 将赎回token转给用户
    _response: Bytes[32] = raw_call(
        self.coins[i],
        concat(
            method_id("transfer(address,uint256)"),
            convert(msg.sender, bytes32),
            convert(dy, bytes32),
        ),
        max_outsize=32,
    )
    if len(_response) > 0:
        assert convert(_response, bool)

    log RemoveLiquidityOne(msg.sender, _token_amount, dy, total_supply - _token_amount)

    return dy

Admin functions

管理员调用的方法

A's adjustment

A 参数的调整，传入目标值 _future_A，预定调整结束时间 _future_time。

当调用 ramp_A() 后，A 参数会随时间线性改变，直到 _future_time 完成调整，达到预设的目标值。这期间池子的计算涉及 A 值都会线性的计算当前值。

调整期间管理员可以调用 stop_ramp_A 终止调整进度，A 会保持当前的值。

@external
def ramp_A(_future_A: uint256, _future_time: uint256):
    assert msg.sender == self.owner  # dev: only owner
    assert block.timestamp >= self.initial_A_time + MIN_RAMP_TIME
    assert _future_time >= block.timestamp + MIN_RAMP_TIME  # dev: insufficient time

    initial_A: uint256 = self._A()
    future_A_p: uint256 = _future_A * A_PRECISION

    assert _future_A > 0 and _future_A < MAX_A
    if future_A_p < initial_A:
        assert future_A_p * MAX_A_CHANGE >= initial_A
    else:
        assert future_A_p <= initial_A * MAX_A_CHANGE

    self.initial_A = initial_A
    self.future_A = future_A_p
    self.initial_A_time = block.timestamp
    self.future_A_time = _future_time

    log RampA(initial_A, future_A_p, block.timestamp, _future_time)


@external
def stop_ramp_A():
    assert msg.sender == self.owner  # dev: only owner

    current_A: uint256 = self._A()
    self.initial_A = current_A
    self.future_A = current_A
    self.initial_A_time = block.timestamp
    self.future_A_time = block.timestamp
    # now (block.timestamp < t1) is always False, so we return saved A

    log StopRampA(current_A, block.timestamp)

fee's adjustment

fee 和 admin fee 的调整

  1. 管理员提交调整方案 commit_new_fee()
    • 如果期间有其他待执行的方案，将不能提交
    • assert self.admin_actions_deadline == 0
    • 自动设置最早执行时间为 block.timestamp + ADMIN_ACTIONS_DELAY
    • ADMIN_ACTIONS_DELAY = 3 * 86400 s 即等待期 3 天
  2. 在等待期过后，管理员执行 apply_new_fee() 让新的费率参数生效
    • 根据 admin_actions_deadline 是否为零判断当前是否有待执行方案
    • assert self.admin_actions_deadline != 0
  3. 等待期间，管理员可调用 revert_new_parameters() 取消调整方案
@external
def commit_new_fee(_new_fee: uint256, _new_admin_fee: uint256):
    assert msg.sender == self.owner  # dev: only owner
    assert self.admin_actions_deadline == 0  # dev: active action
    assert _new_fee <= MAX_FEE  # dev: fee exceeds maximum
    assert _new_admin_fee <= MAX_ADMIN_FEE  # dev: admin fee exceeds maximum

    deadline: uint256 = block.timestamp + ADMIN_ACTIONS_DELAY
    self.admin_actions_deadline = deadline
    self.future_fee = _new_fee
    self.future_admin_fee = _new_admin_fee

    log CommitNewFee(deadline, _new_fee, _new_admin_fee)


@external
def apply_new_fee():
    assert msg.sender == self.owner  # dev: only owner
    assert block.timestamp >= self.admin_actions_deadline  # dev: insufficient time
    assert self.admin_actions_deadline != 0  # dev: no active action

    self.admin_actions_deadline = 0
    fee: uint256 = self.future_fee
    admin_fee: uint256 = self.future_admin_fee
    self.fee = fee
    self.admin_fee = admin_fee

    log NewFee(fee, admin_fee)


@external
def revert_new_parameters():
    assert msg.sender == self.owner  # dev: only owner

    self.admin_actions_deadline = 0

ownership

移交合约 owner。与手续费调整类似，先提交方案，等待期过后，才能执行方案。

@external
def commit_transfer_ownership(_owner: address):
    assert msg.sender == self.owner  # dev: only owner
    assert self.transfer_ownership_deadline == 0  # dev: active transfer

    deadline: uint256 = block.timestamp + ADMIN_ACTIONS_DELAY
    self.transfer_ownership_deadline = deadline
    self.future_owner = _owner

    log CommitNewAdmin(deadline, _owner)


@external
def apply_transfer_ownership():
    assert msg.sender == self.owner  # dev: only owner
    assert block.timestamp >= self.transfer_ownership_deadline  # dev: insufficient time
    assert self.transfer_ownership_deadline != 0  # dev: no active transfer

    self.transfer_ownership_deadline = 0
    owner: address = self.future_owner
    self.owner = owner

    log NewAdmin(owner)

@external
def revert_transfer_ownership():
    assert msg.sender == self.owner  # dev: only owner

    self.transfer_ownership_deadline = 0

admin_fee withdraw and donate

提取和捐赠 admin_fee

  • withdraw_admin_fees() 提取协议费，将每种资产分别转给调用者（管理员）

    • admin_fee 的数量没有专门的字段存储，而是通过 合约持有的总量 - 流动性提供者持有的总量(balances) 获得
    • ERC20(coin).balanceOf(self) - self.balances[i]

  • donate_admin_fees() 将未提取的协议费全部捐赠给池子的流动性提供者

    • self.balances[i] = ERC20(self.coins[i]).balanceOf(self)
    • 上述操作实质上是将协议费的数量清零，全部转移到 balances 上
@view
@external
def admin_balances(i: uint256) -> uint256:
    return ERC20(self.coins[i]).balanceOf(self) - self.balances[i]


@external
def withdraw_admin_fees():
    assert msg.sender == self.owner  # dev: only owner

    for i in range(N_COINS):
        coin: address = self.coins[i]
        value: uint256 = ERC20(coin).balanceOf(self) - self.balances[i]
        if value > 0:
            _response: Bytes[32] = raw_call(
                coin,
                concat(
                    method_id("transfer(address,uint256)"),
                    convert(msg.sender, bytes32),
                    convert(value, bytes32),
                ),
                max_outsize=32,
            )  # dev: failed transfer
            if len(_response) > 0:
                assert convert(_response, bool)


@external
def donate_admin_fees():
    assert msg.sender == self.owner  # dev: only owner
    for i in range(N_COINS):
        self.balances[i] = ERC20(self.coins[i]).balanceOf(self)

kill_me

  • kill_me() 停止合约交易和增减流动性功能
  • unkill_me() 重新开启交易和增加流动性功能

当 is_killed 为 true 时，合约不能运行下列方法：

  • add_liquidity()
  • exchange()
  • remove_liquidity_imbalance()
  • remove_liquidity_one_coin()

注意：remove_liquidity 是可以运行的，允许流动性提供者撤走流动性，但期间不能发生交易行为，即必须按照当前价格移除流动性。

@external
def kill_me():
    assert msg.sender == self.owner  # dev: only owner
    assert self.kill_deadline > block.timestamp  # dev: deadline has passed
    self.is_killed = True


@external
def unkill_me():
    assert msg.sender == self.owner  # dev: only owner
    self.is_killed = False

a-pool and y-pool

相比于base-pool, a-pool 与 y-pool 主要由于其对应的token并不是标准的ERC20，需要做一些适配。

  • a-pool 对应aToken类型，其 balanceOf() 返回的余额不是标准的balance，而是计算了累加利息的数量
  • y-pool 对应 yearn 和 Compound 的 CToken，其兑换底层资产的汇率会改变
  • 在 base pool 中， RATES 将只起到统一精度的作用，但在 y-pool 和 a-pool 中 RATES 不但要统一精度，还需要从外部合约获取 coin 和其底层资产之间的汇率

a-pool

这里以 StableSwapAave.vy 作为解析示例(使用a模板创建)

y-pool

这里以 StableSwapCompound.vy 作为解析示例(使用y模板创建)

  • 在 Compound pool 中，RATES 将从 cERC20.exchangeRateStored() 外部合约方法中，获取 CToken 与其对应的底层资产的汇率
  • 因为 CToken 是一种内增值的 ERC20 变种 token，每单位 CToken 所能兑换的对应底层资产将随着借贷利息的累加而不同
  • _xp(rates) 的定义和base-pool不同，RATES使用传入的值，即 cERC20.exchangeRateStored()
# contracts/pools/compound/StableSwapCompound.vy

@private
@constant
def _stored_rates() -> uint256[N_COINS]:
    # exchangeRateStored * (1 + supplyRatePerBlock * (getBlockNumber - accrualBlockNumber) / 1e18)
    result: uint256[N_COINS] = PRECISION_MUL
    use_lending: bool[N_COINS] = USE_LENDING
    for i in range(N_COINS):
        rate: uint256 = LENDING_PRECISION  # Used with no lending
        if use_lending[i]:
            rate = cERC20(self.coins[i]).exchangeRateStored() # 这里获取最新的汇率
            supply_rate: uint256 = cERC20(self.coins[i]).supplyRatePerBlock()
            old_block: uint256 = cERC20(self.coins[i]).accrualBlockNumber()
            rate += rate * supply_rate * (block.number - old_block) / LENDING_PRECISION
        result[i] *= rate
    return result

@private
@constant
def _xp(rates: uint256[N_COINS]) -> uint256[N_COINS]:
    result: uint256[N_COINS] = rates # rates通过入参传入
    for i in range(N_COINS):
        result[i] = result[i] * self.balances[i] / PRECISION
    return result